Question

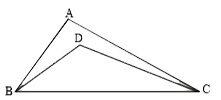
In a triangle ABC, the median BD yields $\angle BDC={45}^{\circ }$ and $\angle ABD=\angle BCD=x^{\circ }$. Find the value of x.

Options

A. `45^@`
B. `30^@`
C. `60^@`
D. none of these

Answer

A

Explanation

To solve the problem, we need to find the value of $$x$$ in triangle $$ABC$$ given the conditions about the angles.

1. Identify the Angles:
- We are given that \( \angle BDC = 45^\circ \).
- We also know that \( \angle ABD = \angle BCD = x^\circ \).

2. Use the Triangle Angle Sum Property:
- In triangle \( ABD \), the sum of the angles is \( 180^\circ \).
- Therefore, we can write the equation for the angles in triangle \( ABD \):
\( \angle ABD + \angle ADB + \angle DAB = 180^\circ \)
- Substituting the known angles, we have:
\( x + \angle ADB + \angle DAB = 180^\circ \)

3. Express \( \angle ADB \) and \( \angle DAB \):
- Since \( BD \) is a median, \( D \) divides \( AC \) into two equal parts.
- This means that \( \angle ADB \) and \( \angle DAB \) can be expressed in terms of \( x \) and \( 45^\circ \).
- Specifically, \( \angle ADB = 45^\circ \) and \( \angle DAB = x \).

4. Set Up the Equation:
- Now substituting back into the angle sum equation:
\( x + 45^\circ + x = 180^\circ \)
- Simplifying this gives:
\( 2x + 45^\circ = 180^\circ \)

5. Solve for \( x \):
- Rearranging the equation:
\( 2x = 180^\circ - 45^\circ \)
\( 2x = 135^\circ \)
- Dividing both sides by 2:
\( x = \frac{135^\circ}{2} = 67.5^\circ \)

Conclusion:
The value of \( x \) is \( 67.5^\circ \).