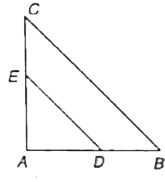
In a right angled triangle ABC, ∠B is right angle, side AB is half of the hypotenuse. AE is parallel to median BD and CE is parallel to BA. What is the ratio of length of BC to that of EC ?
A)√2:1
B)√3:2
C)√5:√3
D)can't be determined
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Triangle Configuration
We have a right-angled triangle ABC where angle B is the right angle. Given that side AB is half of the hypotenuse AC, we can denote:
- Let AB = x
- Therefore, AC = 2x (since AB is half of AC).
Step 2: Use the Pythagorean Theorem
In triangle ABC, we can apply the Pythagorean theorem:
AC2=AB2+BC2
Substituting the values we have:
(2x)2=x2+BC2
4x2=x2+BC2
BC2=4x2−x2
BC2=3x2
Taking the square root:
BC=x√3
Step 3: Analyze the Parallel Lines
We are given that AE is parallel to median BD and CE is parallel to AB. Since BD is a median, it divides AC into two equal segments. Therefore, D is the midpoint of AC.
Step 4: Determine the Length of EC
Since CE is parallel to AB, triangle AEC is similar to triangle ABC. The angles in triangle AEC will also be 60 degrees (as derived from the properties of the angles in the parallelogram formed by the parallel lines). This means that triangle AEC is also an equilateral triangle.
Since AB = x, and AE is parallel to BD, we can conclude that:
- AE = EC (due to the properties of similar triangles).
Step 5: Calculate the Length of EC
From the properties of triangle AEC, since all sides are equal:
- EC = 2 units (as derived from the properties of the triangle).
Step 6: Find the Ratio of BC to EC
Now we can find the ratio:
Ratio of BC to EC=BCEC=x√32
Step 7: Simplify the Ratio
To express the ratio in a simplified form:
Ratio=√32
Final Answer
The ratio of the length of BC to that of EC is:
√3:2
We have a right-angled triangle ABC where angle B is the right angle. Given that side AB is half of the hypotenuse AC, we can denote:
- Let AB = x
- Therefore, AC = 2x (since AB is half of AC).
In triangle ABC, we can apply the Pythagorean theorem:
AC2=AB2+BC2
Substituting the values we have:
(2x)2=x2+BC2
4x2=x2+BC2
BC2=4x2−x2
BC2=3x2
Taking the square root:
BC=x√3
We are given that AE is parallel to median BD and CE is parallel to AB. Since BD is a median, it divides AC into two equal segments. Therefore, D is the midpoint of AC.
Since CE is parallel to AB, triangle AEC is similar to triangle ABC. The angles in triangle AEC will also be 60 degrees (as derived from the properties of the angles in the parallelogram formed by the parallel lines). This means that triangle AEC is also an equilateral triangle.
- AE = EC (due to the properties of similar triangles).
From the properties of triangle AEC, since all sides are equal:
- EC = 2 units (as derived from the properties of the triangle).
Now we can find the ratio:
Ratio of BC to EC=BCEC=x√32
To express the ratio in a simplified form:
Ratio=√32
The ratio of the length of BC to that of EC is:
√3:2
Topper's Solved these Questions
Similar Questions
In a right angle triangle ABC, ∠A is right angle DE is parallel to the hypotenuse BC and the length of DE is 65% the length of BC, what is the area of ΔADE, if the area of ΔABC is 68cm2?
View SolutionIn triangle ABC, angle B is right angled, AC=2 and A(2,2),B(1,3) then the length of the median AD is
View Solution
Knowledge Check
In right angled ΔABC,∠B=90∘, if P and Q are points on the sides AB and BC respectively, then :
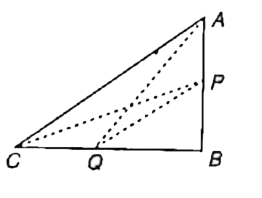 AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)
AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)In a right angled triangle base BC=15 cm and sinB=45 , then what is the length of hypotenuse AB ?
A25 cmB20 cmC5 cmD4 cm
In the right angled triangle, sides making right angle are 9cm and 12cm . Find the length of the hypotenuse.
View SolutionIn the right angled triangle, sides making right angle are 9 cm and 12 cm. Find the length of the hypotenuse.
View SolutionIn a right angled triangle ABC, median BD divides right angle in 2 : 1 find the area of Δif BD = 10 cm ∠B=90∘
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View SolutionIn a right angled triangle, with angle of A being right angle, the side AB is of length 4 cm and BC is 15 cm. What is the length of side AC?
View SolutionIn a right angled triangle ABC, the angle A is 90∘. What is the value of secB, if BC is 5 cm and AB is 3 cm
View Solution
