A fox, camouflaged in the bush, observes from the ground, that it takes 2 minutes for the angle of elevation of the squirrel to change from 30∘ to 60∘. If the speed of fox is √3 times that of the squirrel, find the time taken by fox to reach the tree from the bush.
1 minute
√3 minute
3 minute
4√3 minute
The correct Answer is:A
To solve the problem, we will break it down into steps.
Step 1: Understand the scenario
The fox observes the squirrel from the ground. The angle of elevation changes from 30∘ to 60∘ over a period of 2 minutes. We need to find the time taken by the fox to reach the tree where the squirrel is.
Step 2: Set up the right triangles
Let:
- AB be the height of the tree (the vertical distance from the ground to the squirrel).
- BC be the horizontal distance from the fox to the base of the tree when the angle of elevation is 30∘.
- CE be the horizontal distance from the fox to the base of the tree when the angle of elevation is 60∘.
Step 3: Use trigonometric ratios
For the first triangle ABC (when the angle of elevation is 30∘):
tan(30∘)=ABBC⟹1√3=ABBC⟹AB=BC√3(1)
For the second triangle DCE (when the angle of elevation is 60∘):
tan(60∘)=DECE⟹√3=DECE⟹DE=√3⋅CE(2)
Since AB=DE, we can equate (1) and (2):
BC√3=√3⋅CE
Step 4: Solve for the distances
Cross-multiplying gives:
BC=3⋅CE(3)
Step 5: Determine the distance traveled by the squirrel
The squirrel moves from point C to point E in 2 minutes. The distance CE is 1 unit (from the ratio derived earlier) and BC is 3 units. Therefore, the distance traveled by the squirrel is:
BE=BC−CE=3−1=2 units
Step 6: Calculate the speed of the squirrel
The speed of the squirrel is:
Speed of squirrel=DistanceTime=2 units2 minutes=1 unit/minute
Step 7: Calculate the speed of the fox
The speed of the fox is given as √3 times the speed of the squirrel:
Speed of fox=√3⋅1=√3 units/minute
Step 8: Calculate the time taken by the fox to reach the tree
The distance the fox needs to cover is BC which is 3 units. The time taken by the fox is:
Time=DistanceSpeed=3 units√3 units/minute=√3 minutes
Final Answer
The time taken by the fox to reach the tree from the bush is √3 minutes.
---
The fox observes the squirrel from the ground. The angle of elevation changes from 30∘ to 60∘ over a period of 2 minutes. We need to find the time taken by the fox to reach the tree where the squirrel is.
Let:
- AB be the height of the tree (the vertical distance from the ground to the squirrel).
- BC be the horizontal distance from the fox to the base of the tree when the angle of elevation is 30∘.
- CE be the horizontal distance from the fox to the base of the tree when the angle of elevation is 60∘.
For the first triangle ABC (when the angle of elevation is 30∘):
tan(30∘)=ABBC⟹1√3=ABBC⟹AB=BC√3(1)
tan(60∘)=DECE⟹√3=DECE⟹DE=√3⋅CE(2)
Since AB=DE, we can equate (1) and (2):
BC√3=√3⋅CE
Cross-multiplying gives:
BC=3⋅CE(3)
The squirrel moves from point C to point E in 2 minutes. The distance CE is 1 unit (from the ratio derived earlier) and BC is 3 units. Therefore, the distance traveled by the squirrel is:
BE=BC−CE=3−1=2 units
The speed of the squirrel is:
Speed of squirrel=DistanceTime=2 units2 minutes=1 unit/minute
The speed of the fox is given as √3 times the speed of the squirrel:
Speed of fox=√3⋅1=√3 units/minute
The distance the fox needs to cover is BC which is 3 units. The time taken by the fox is:
Time=DistanceSpeed=3 units√3 units/minute=√3 minutes
The time taken by the fox to reach the tree from the bush is √3 minutes.
Topper's Solved these Questions
Similar Questions
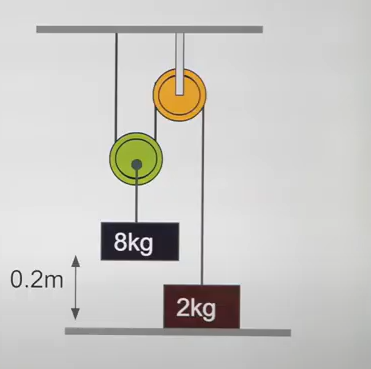
If the system is left from rest find the time taken by the 8kg block to reach the ground.
View SolutionA person from the top of a hill observes a vehicle moving towards him at a uniform speed. It takes 10 minutes for the angle of depression to change from 45∘ to 60∘. After this the time required by the vehicle to reach the bottom of the hill is:
View Solution
Knowledge Check
A man on the top of a vertical tower observes a car moving at a uniform speed towards the tower on a horizontal road. If it takes 18 minutes from the angle of depression of the car to change from 30∘to45∘, then after this, the time taken (in minutes) by the car to reach the foot of the tower, is
A9(1+√3)B18(√3−1)C92(√3−1)D18(1+√3
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car change from 30∘ and 45∘ in 12 minutes, find the time taken by the car now toreach the tower.
View SolutionA man on the top of a tower, standing on the seashore, finds that a boat coming towards him takes 10 minutes for the angle of depression to change from 30o to 60o . Find the time taken by the boat to reach the shore from the position.
View SolutionA man on the top of a tower: standing on the seashore: finds that a boat coming towards him takes 10 min for the angle of depression to change from 30∘ to 60∘. Find the time taken by the boat to reach the shore from this position
View SolutionA man in a boat rowing away from a light house 100 m high takes 2 minutes to change the angle of elevation of the top of the light house from 60° to 30°. Find the speed of the boat in meters per minute. [Use √3=1.732)
View SolutionA moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60∘ to 45∘ in 2 minutes. Find the speed of the boat in m/h.
View SolutionIf the angle of elevation of top of a tower from a point on the ground which is 20√3 m away from the foot of the tower is 30∘, then find the height of the tower.
View SolutionA man in a boat rowed away from a cliff 150 m high takes 2 min, to change the angle from 60∘ to 45∘. The speed of the boat is
View Solution
