A number is expressed as 2m×3n and the sum of all its factors is 124, find m and n.
2, 3
3, 1
4,1
3, 2
The correct Answer is:C
To solve the problem, we need to find the values of m and n such that the number expressed as 2m×3n has a sum of all its factors equal to 124.
1. Understanding the Sum of Factors Formula:
The sum of the factors of a number N=pk11×pk22 is given by the formula:
σ(N)=(1+p1+p21+…+pk11)(1+p2+p22+…+pk22)
For our case, where N=2m×3n, the sum of the factors can be expressed as:
σ(N)=(1+2+22+…+2m)(1+3+32+…+3n)
2. Calculating Each Part:
The first part can be calculated using the formula for the sum of a geometric series:
1+2+22+…+2m=2m+1−12−1=2m+1−1
The second part is:
1+3+32+…+3n=3n+1−13−1=3n+1−12
3. Setting Up the Equation:
Now, we can set up the equation for the sum of the factors:
σ(N)=(2m+1−1)(3n+1−12)=124
Multiplying both sides by 2 to eliminate the fraction:
(2m+1−1)(3n+1−1)=248
4. Finding Factor Pairs of 248:
Next, we need to find pairs of factors of 248. The factor pairs of 248 are:
- (1, 248)
- (2, 124)
- (4, 62)
- (8, 31)
- (16, 15)
5. Testing Each Factor Pair:
We will test each factor pair to see if they can be expressed in the form (2m+1−1) and (3n+1−1).
- For the factor pair (8, 31):
2m+1−1=8⟹2m+1=9⟹m+1=3⟹m=2
3n+1−1=31⟹3n+1=32⟹n+1=5⟹n=4
- Check if m=2 and n=4 satisfy the original sum of factors:
σ(N)=(22+1−1)(34+1−1)=(8−1)(243−1)=7×242=1694(not valid)
- For the factor pair (4, 62):
2m+1−1=4⟹2m+1=5⟹m+1=3⟹m=2
3n+1−1=62⟹3n+1=63⟹n+1=3⟹n=2
- Check if m=2 and n=2 satisfy the original sum of factors:
σ(N)=(22+1−1)(32+1−1)=(8−1)(27−1)=7×26=182(not valid)
- For the factor pair (16, 15):
2m+1−1=16⟹2m+1=17⟹m+1=5⟹m=4
3n+1−1=15⟹3n+1=16⟹n+1=4⟹n=3
- Check if m=4 and n=3 satisfy the original sum of factors:
σ(N)=(24+1−1)(33+1−1)=(32−1)(81−1)=31×80=248(valid)
6. Conclusion:
The values of m and n that satisfy the condition are:
m=4,n=3
The sum of the factors of a number N=pk11×pk22 is given by the formula:
σ(N)=(1+p1+p21+…+pk11)(1+p2+p22+…+pk22)
For our case, where N=2m×3n, the sum of the factors can be expressed as:
σ(N)=(1+2+22+…+2m)(1+3+32+…+3n)
The first part can be calculated using the formula for the sum of a geometric series:
1+2+22+…+2m=2m+1−12−1=2m+1−1
The second part is:
1+3+32+…+3n=3n+1−13−1=3n+1−12
Now, we can set up the equation for the sum of the factors:
σ(N)=(2m+1−1)(3n+1−12)=124
Multiplying both sides by 2 to eliminate the fraction:
(2m+1−1)(3n+1−1)=248
Next, we need to find pairs of factors of 248. The factor pairs of 248 are:
- (1, 248)
- (2, 124)
- (4, 62)
- (8, 31)
- (16, 15)
We will test each factor pair to see if they can be expressed in the form (2m+1−1) and (3n+1−1).
2m+1−1=8⟹2m+1=9⟹m+1=3⟹m=2
3n+1−1=31⟹3n+1=32⟹n+1=5⟹n=4
σ(N)=(22+1−1)(34+1−1)=(8−1)(243−1)=7×242=1694(not valid)
2m+1−1=4⟹2m+1=5⟹m+1=3⟹m=2
3n+1−1=62⟹3n+1=63⟹n+1=3⟹n=2
σ(N)=(22+1−1)(32+1−1)=(8−1)(27−1)=7×26=182(not valid)
2m+1−1=16⟹2m+1=17⟹m+1=5⟹m=4
3n+1−1=15⟹3n+1=16⟹n+1=4⟹n=3
σ(N)=(24+1−1)(33+1−1)=(32−1)(81−1)=31×80=248(valid)
The values of m and n that satisfy the condition are:
m=4,n=3
Topper's Solved these Questions
Similar Questions
For any natural number n, expressed in base 10, let S(n) denote the sum of all digits of n. Find all natural numbers n such that n3=8S(n)3+6nS(n)+1.
View SolutionFor any natural n , expressed in base 10, let S(n) denote the sum of all digits of n. Find all natural numbers n such that n = 2S(n)2 ?
View Solution
Knowledge Check
A natural number N is such that 1010<N<1010 and the sum of its digits is 3. Find the total number of values of N.
A121B111C222D144For any natural number n, if D (n) is the sum of all the digits of D(n) find the remainder when 99∑1 D(n) is divided by 99.
A9B0C1D90For any natural number n, if D (n) is the sum of all the digits of D(n) find the remainder when 99∑1 D(n) is divided by 99.
A9B0C1D89
The sum of all the prime factors of m is 9. Find the number m.
View SolutionIn the adjoining factor tree, find the numbers m and n.
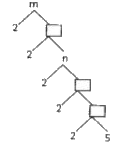
View SolutionIn the adjoining factor tree, find the numbers m and n

View SolutionIn an AP, the sum of first n terms is n2+2n. Find its 18th term.
View SolutionA number n is said to be 'perfect' if the sum of all its divisors excluding n 'itself' is equal to n. An example of perfect number is :
View Solution
