Find the value of
(53)3
To find the value of (53)3, we can use the identity for the cube of a binomial, which states:
(a+b)3=a3+b3+3ab(a+b)
1. Identify a and b:
Let a=50 and b=3. Therefore, we can rewrite 53 as 50+3.
2. Apply the identity:
Using the identity, we have:
(50+3)3=503+33+3⋅50⋅3⋅(50+3)
3. Calculate 503:
503=125000
4. Calculate 33:
33=27
5. Calculate 3⋅50⋅3⋅(50+3):
First, calculate 50+3=53.
Then, calculate:
3⋅50⋅3⋅53=9⋅50⋅53
Now, calculate 50⋅53:
50⋅53=2650
Therefore:
9⋅2650=23850
6. Combine all parts:
Now, we can combine all the calculated parts:
125000+27+23850
7. Add them together:
First, add 125000+27=125027.
Then, add 125027+23850=148877.
Thus, the value of (53)3 is:
148877
Let a=50 and b=3. Therefore, we can rewrite 53 as 50+3.
Using the identity, we have:
(50+3)3=503+33+3⋅50⋅3⋅(50+3)
503=125000
33=27
First, calculate 50+3=53.
Then, calculate:
3⋅50⋅3⋅53=9⋅50⋅53
Now, calculate 50⋅53:
50⋅53=2650
Therefore:
9⋅2650=23850
Now, we can combine all the calculated parts:
125000+27+23850
First, add 125000+27=125027.
Then, add 125027+23850=148877.
148877
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the value of ∣∣∣53−7−4∣∣∣
A−1B−41C41D1
Find the value of 10−3,6−5,33
View SolutionThe mean of the following data is 53, Find the value of f1andf2
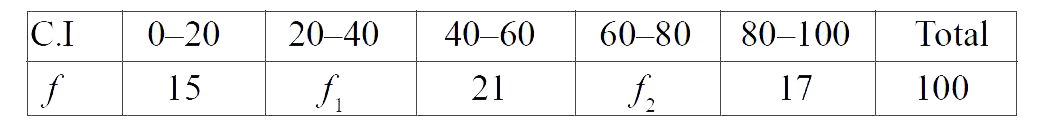
View SolutionFind the value of : C(5,1)+C(5,2)+C(5,3)+C(5,4)
View SolutionMean of six observations 30, 68, 72, 53, 87 and x is 60. Find the value of x.
View Solution51+53+55+...+tn=5151.Then find the value of tn
View Solution51+53+55+...+tn=5151 Then find the value of tn
View SolutionShow that A=[53−1−2] satisfies the equation A2−3A−7I=0 and hence find the value of A−1
View Solution
