A certain amount of water of mass m, at a temperature T2 cools.to temperature T1. The heat given out by the water is absorbed by n mole of an ideal gas. The gas expands at constant temperature T and changes its volume from Vi to Vf What is its initial volume ?
To find the initial volume Vi of the ideal gas that absorbs the heat given out by the cooling water, we can follow these steps:
1. Calculate the Heat Lost by Water:
The heat lost by the water as it cools from temperature T2 to T1 can be calculated using the formula:
Q=mc(T2−T1)
where:
- m = mass of the water
- c = specific heat capacity of water
- T2 = initial temperature of the water
- T1 = final temperature of the water
2. Relate Heat to Work Done by the Gas:
For an ideal gas expanding isothermally, the work done W is given by:
W=nRTln(VfVi)
where:
- n = number of moles of the gas
- R = universal gas constant
- T = constant temperature during the expansion
- Vf = final volume of the gas
- Vi = initial volume of the gas
3. Set Heat Lost Equal to Work Done:
Since the heat lost by the water is equal to the work done by the gas, we can write:
mc(T2−T1)=nRTln(VfVi)
4. Rearranging the Equation:
We can rearrange the equation to isolate the logarithmic term:
ln(VfVi)=mc(T2−T1)nRT
5. Exponentiate to Solve for Volume Ratio:
By exponentiating both sides, we obtain:
VfVi=emc(T2−T1)nRT
6. Solve for Initial Volume Vi:
Finally, we can express Vi in terms of Vf:
Vi=Vf⋅e−mc(T2−T1)nRT
Final Answer:
The initial volume Vi of the ideal gas is given by:
Vi=Vf⋅e−mc(T2−T1)nRT
The heat lost by the water as it cools from temperature T2 to T1 can be calculated using the formula:
Q=mc(T2−T1)
where:
- m = mass of the water
- c = specific heat capacity of water
- T2 = initial temperature of the water
- T1 = final temperature of the water
For an ideal gas expanding isothermally, the work done W is given by:
W=nRTln(VfVi)
where:
- n = number of moles of the gas
- R = universal gas constant
- T = constant temperature during the expansion
- Vf = final volume of the gas
- Vi = initial volume of the gas
Since the heat lost by the water is equal to the work done by the gas, we can write:
mc(T2−T1)=nRTln(VfVi)
We can rearrange the equation to isolate the logarithmic term:
ln(VfVi)=mc(T2−T1)nRT
By exponentiating both sides, we obtain:
VfVi=emc(T2−T1)nRT
Finally, we can express Vi in terms of Vf:
Vi=Vf⋅e−mc(T2−T1)nRT
The initial volume Vi of the ideal gas is given by:
Vi=Vf⋅e−mc(T2−T1)nRT
Topper's Solved these Questions
- INTERNAL ENERGY Book:ICSEChapter:INTERNAL ENERGY Exercise:SOLVED EXAMPLES
Explore 9 Videos
- INTERNAL ENERGY Book:ICSEChapter:INTERNAL ENERGY Exercise:ADDITIONAL SOLVED PROBLEMS
Explore 12 Videos
- GRAVITATIONBook:ICSEChapter:GRAVITATIONExercise:FROM THE HUBBLE TELESCOP
Explore 2 Videos
- MOTION IN FLUIDS Book:ICSEChapter:MOTION IN FLUIDS Exercise:SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
Explore 19 Videos
Similar Questions
For a sample of n mole of a perfect gas at constant temperature T (K) when its volume is changed from V1 to V2 the entropy change is given by
View SolutionThe raise in the temperature of a given mass of an ideal gas at constant pressure and at temperature 27∘ to double its volume is
View SolutionTemperature of an ideal gas is 300 K. The change in temperature of the gas when its volume changes from V to 2V in the process p = aV (Here, a is a positive constant) is
View SolutionWhen a certain amount of heat is supplied to a diatomic gas at constant volume, rise in temperature is T0. When same heat is supplied to the gas at constant pressure, find the rise in temperature
View SolutionWhich of the following volume-temperature (V−T) plots represents the behaviour of 1mole of an ideal gas at the atmospheric pressure?
View SolutionWhich of the following volume (V) –temperature (T) plots represents the behaviour of one mole of an ideal gas at one atmospheric pressure?
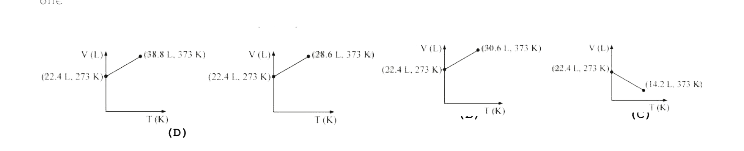
View SolutionDuring an experiment, an ideal gas is found to obey an additional law pV2=constant. The gas is initially at a temperature T and volume V. Find the temperature when it expands to a volume 2V.
View SolutionAn ideal gas expands adiabatically from an initial temperature T1 to a final temperature T2. Prove that the work done by the gas is CV(T1−T2).
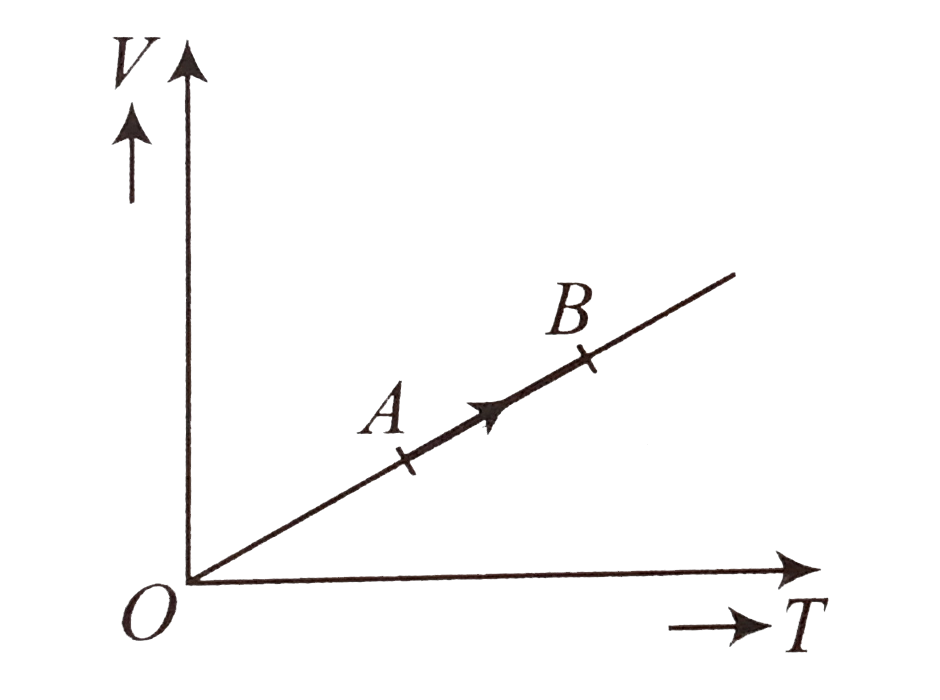
View SolutionThe volume (V) of a monatomic gas varies with its temperature (T) as shown in the graph. The ratio of work done by the gas, to the heat absorbed by it, when it undergoes a change from state A to state B,is
View SolutionOne mole of ideal gas goes through processP=2V21+V2. Then change in temperature of gas when volume changes from V=1m2 to 2m2 is :
View Solution