Two simple pendulums of equal length cross each other at mean position. What is their phase difference ?
To solve the problem of finding the phase difference between two simple pendulums of equal length that cross each other at the mean position, we can follow these steps:
1. Understanding Simple Pendulum Motion:
- A simple pendulum exhibits simple harmonic motion (SHM) when it swings back and forth. The motion can be described in terms of sine or cosine functions, which represent the displacement of the pendulum over time.
2. Mean Position:
- The mean position of a pendulum is the point where it hangs vertically downwards (the equilibrium position). At this position, the pendulum has maximum speed and zero displacement.
3. Crossing at Mean Position:
- When two pendulums cross each other at the mean position, it means they are both passing through the equilibrium point simultaneously.
4. Phase of Simple Harmonic Motion:
- The phase of a simple harmonic motion can be represented as a function of time. For two pendulums oscillating with the same frequency and amplitude, their positions can be described as:
- x1(t)=Asin(ωt) for the first pendulum.
- x2(t)=Asin(ωt+ϕ) for the second pendulum, where ϕ is the phase difference.
5. Determining the Phase Difference:
- When both pendulums cross the mean position, their displacements are both zero. This occurs when:
- For the first pendulum: sin(ωt)=0
- For the second pendulum: sin(ωt+ϕ)=0
- The sine function is zero at integer multiples of π. Therefore, if one pendulum is at zero displacement, the other must also be at zero displacement but could be at a different point in its cycle.
6. Conclusion on Phase Difference:
- Since the two pendulums are moving in opposite directions when they cross the mean position, the phase difference between them is π radians (or 180 degrees).
Final Answer:
The phase difference between the two simple pendulums when they cross each other at the mean position is π radians or 180 degrees.
---
- A simple pendulum exhibits simple harmonic motion (SHM) when it swings back and forth. The motion can be described in terms of sine or cosine functions, which represent the displacement of the pendulum over time.
- The mean position of a pendulum is the point where it hangs vertically downwards (the equilibrium position). At this position, the pendulum has maximum speed and zero displacement.
- When two pendulums cross each other at the mean position, it means they are both passing through the equilibrium point simultaneously.
- The phase of a simple harmonic motion can be represented as a function of time. For two pendulums oscillating with the same frequency and amplitude, their positions can be described as:
- x1(t)=Asin(ωt) for the first pendulum.
- x2(t)=Asin(ωt+ϕ) for the second pendulum, where ϕ is the phase difference.
- When both pendulums cross the mean position, their displacements are both zero. This occurs when:
- For the first pendulum: sin(ωt)=0
- For the second pendulum: sin(ωt+ϕ)=0
- The sine function is zero at integer multiples of π. Therefore, if one pendulum is at zero displacement, the other must also be at zero displacement but could be at a different point in its cycle.
- Since the two pendulums are moving in opposite directions when they cross the mean position, the phase difference between them is π radians (or 180 degrees).
The phase difference between the two simple pendulums when they cross each other at the mean position is π radians or 180 degrees.
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (FROM THE CHARACTERISTIC OF SHM)
14 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (FROM ENERGY OF AS.H. OSCILLATOR )
9 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SHORT ANSWER QUESTIONS
47 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
A simple pendulum of length 1 oscillates aboμt the mean position as shown in the figure. If the total energy of the pendulum is E, the velocity of the pendulum bob of mass m at point P is:

View SolutionThe composition of two simple harmonic motions of equal periods at right angle to each other and with a phase difference of π results in the displacement of the particle along
View Solution
Knowledge Check
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2∘ to the right with the vertical , the other pendulum makes an angle of 1∘ to the left of the vertical. What is the phase difference between the pendulums?
Aπ2B23πC32πDπTwo particles execute SHM of same amplitude and same time period, about same mean position but with a phase difference between them. At an instant they are found to cross each other at x=+A3. The phase difference between them is
A2cos−1(15)B2sin−1(15)C2cos−1(13)D2sin−1(15)
The figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
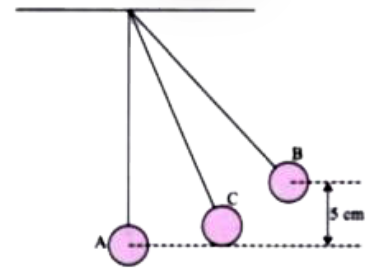
(i) What is the potential energy of the pendulum at the position B?
(ii) What is the total mechanical energy at point C?
(iii) What is the speed of the bob at the position A when released from B ?
(Take g = 10ms−2 and there is no loss of energy.)
View SolutionTwo simple pendulum of length l and 16l are released from the same phase together. They will be at the same time phase after a minimum time.
View SolutionTwo pendulums having time period T and 5T4. They startS.H.M. at the same time from mean position. what will be the phase difference between them after the bigger pendulum has completes one oscillation ?
View SolutionA: The phase difference between the two particles shown below is π. (Assuming both particles have same time periods and same amplitudes).
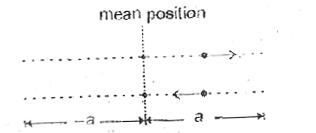
R: If the particles cross each other while they move in the opposite direction, they have a phase difference of π radian.
View SolutionStatement-1 : As a simple pendulum oscillates, its bob has a non-zero acceleration at the mean position which is directed towards the point of suspension.
bacause
Statement -2 : Speed of an object in SHM is maximum at the mean position.
View SolutionIf the second pendulum bob is thrown at velocity v2 at an angle β from mean position, but on other side of mean position , find the phase diffrence in the two SHMs now as show in the figure.

View Solution
