Let a and b be natural numbers and let q and r be the quotient and remainder respectively when a2+b2 is divided by a + b . Determine the number q and r if q2+r=2000.
The correct Answer is:64
To solve the problem, we need to determine the values of q (the quotient) and r (the remainder) when a2+b2 is divided by a+b, given the condition q2+r=2000.
1. Understanding the Division:
When a2+b2 is divided by a+b, we can express it in the form:
a2+b2=(a+b)⋅q+r
where q is the quotient and r is the remainder.
2. Using the Identity:
We can use the identity:
a2+b2=(a+b)2−2ab
This means:
a2+b2=(a+b)⋅q+r
can be rewritten as:
(a+b)2−2ab=(a+b)⋅q+r
3. Finding Quotient and Remainder:
From the equation above, we can see:
- The quotient q=a+b
- The remainder r=−2ab
4. Substituting into the Condition:
We are given the condition:
q2+r=2000
Substituting q and r:
(a+b)2−2ab=2000
5. Simplifying the Equation:
We can rewrite the equation:
(a+b)2−2ab=2000
This simplifies to:
a2+b2=2000
6. Finding Suitable Values for a and b:
We can use trial and error to find natural numbers a and b such that:
a2+b2=2000
Testing pairs:
- Let a=40 and b=20:
402+202=1600+400=2000
This works.
7. Calculating q and r:
Now, we can calculate q and r:
- q=a+b=40+20=60
- r=−2ab=−2⋅40⋅20=−1600
8. Final Values:
Thus, we find:
q=60,r=−1600
Final Answer:
The values of q and r are:
q=60,r=−1600
When a2+b2 is divided by a+b, we can express it in the form:
a2+b2=(a+b)⋅q+r
where q is the quotient and r is the remainder.
We can use the identity:
a2+b2=(a+b)2−2ab
This means:
a2+b2=(a+b)⋅q+r
can be rewritten as:
(a+b)2−2ab=(a+b)⋅q+r
From the equation above, we can see:
- The quotient q=a+b
- The remainder r=−2ab
We are given the condition:
q2+r=2000
Substituting q and r:
(a+b)2−2ab=2000
We can rewrite the equation:
(a+b)2−2ab=2000
This simplifies to:
a2+b2=2000
We can use trial and error to find natural numbers a and b such that:
a2+b2=2000
Testing pairs:
- Let a=40 and b=20:
402+202=1600+400=2000
This works.
Now, we can calculate q and r:
- q=a+b=40+20=60
- r=−2ab=−2⋅40⋅20=−1600
Thus, we find:
q=60,r=−1600
The values of q and r are:
q=60,r=−1600
Topper's Solved these Questions
- NUMBER THEORYBook:RESONANCEChapter:NUMBER THEORYExercise:Self Practice Problems
Explore 5 Videos
- NUMBER THEORYBook:RESONANCEChapter:NUMBER THEORYExercise:Exercise -1 (PART - I)
Explore 30 Videos
- MATRICES & DETERMINANTBook:RESONANCEChapter:MATRICES & DETERMINANTExercise:HLP
Explore 33 Videos
- RELATION, FUNCTION & ITFBook:RESONANCEChapter:RELATION, FUNCTION & ITFExercise:SSP
Explore 55 Videos
Similar Questions
AN IMPORTANT RESULT If a and b are two whole numbers such that q is the quotient and r is the remainder when a is divided by b then
View SolutionFor natural numbers, when p is divided by d, the quotient is q and the remainder is r. When q is divided by d, the quotient is q and the remainder is r'. Then if p is divided by dd' the remainder is
View Solution
Knowledge Check
Let n be a 5-digit number and let q and r be the quotient and remainder respectively, when n is divided by 100. For how many values of n is q+r divisible by 11?
A8180B8181C8182D9000Let N be the set of all natural numbers and let R={(a,b):a,b∈N and 2a+b=10}, The domain and range of R is
Adomain (R ) = {1,2,3,4} and range = {2,4,6,8}Bdomain (R ) = {1,2,3} and range = all natural numbersCdomain (R )={1,2,34} and range = {2,4,6,8}Dnone of theseLet p,qandr be three statements, then (p→q)→r is equivalent to
A(p∨r)∧(q∨r)B(p∨r)∧(~q∨r)C(p∧r)∨(q∨r)D(p∨r)→r
When a certain positive integer P is divided by another positive integer, the remainder is r1 When a second positive integer Q is divided by the same integer, the remainder is r2 and when (P + Q) is divided by the same divisor, the remainder is r3. Then the divsor may be r1 r2 r3 (b) r1+r2+r3 (c) r1−r2+r3 (d) r1 +r2−r3 (e) Ca∩ot be determ∈ed
View SolutionLet R and Q be the sets of real numbers and rational numbers respectively. If a∈Q and fR→R is defined by, f(x)=x when x∈Q,a−x when x not in Q then show that fof(x)=x for all x∈R
View SolutionLet S be set of all numbers and let R be a relation on S defined by aRb⇔a2+b2=1 then, R is
View SolutionLet d + 2(2b + c)=19. What will be the remainder when the 4-digit number abcd is divided by 8?
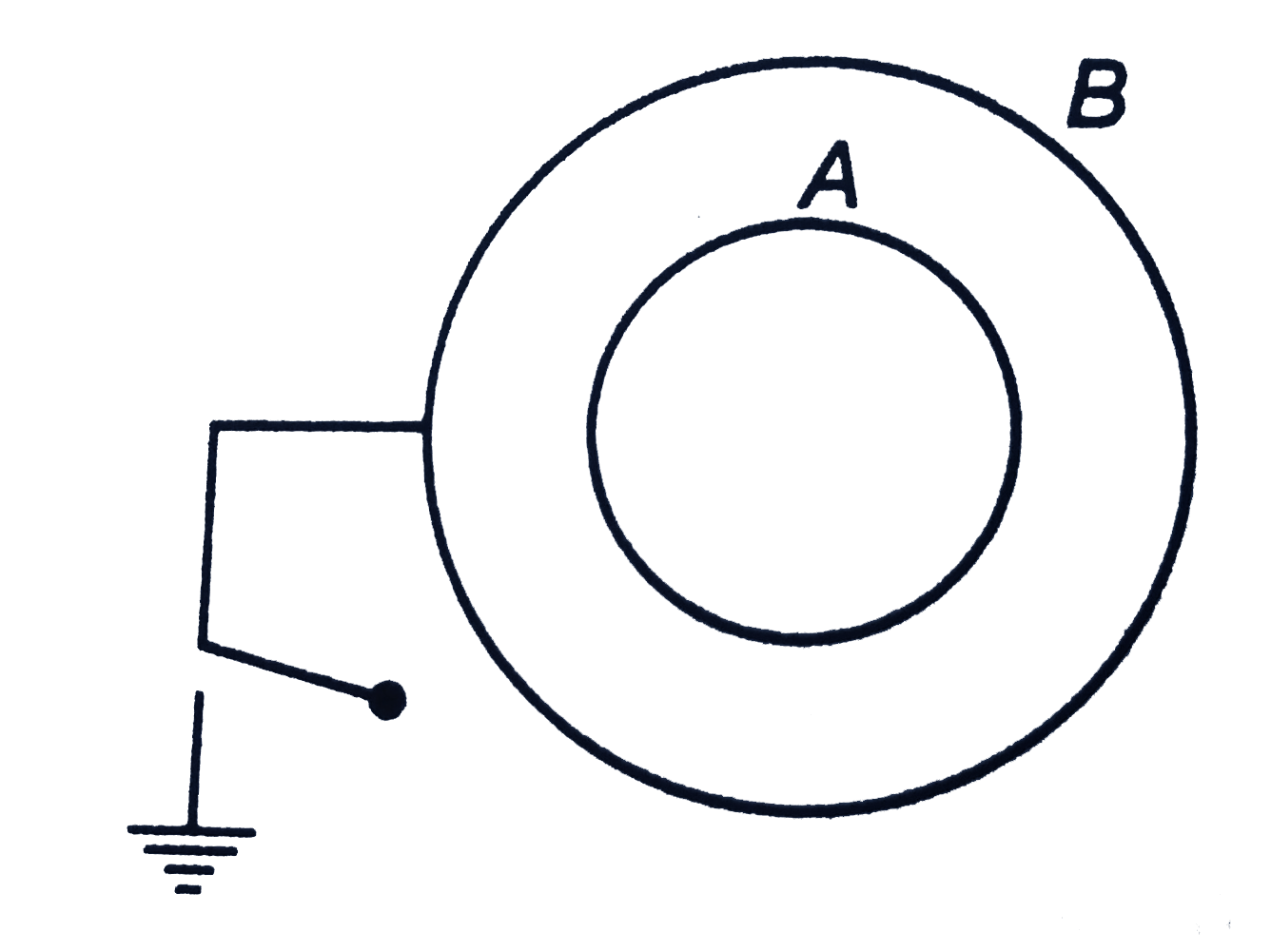
View SolutionTwo concentric shells have radii R and 2R charges qA and qB and potentials 2V and (32)V respectively. Now, shell B is earthed and let charges on them become qA' and qB'. Then,
View Solution
