In Δ ABC, O is the circum centre of the circle. If ∠OBC=37∘ then ∠BAC is equal to :
74∘
106∘
53∘
37∘
The correct Answer is:C
To solve the problem, we need to find the measure of angle BAC in triangle ABC, given that angle OBC is 37 degrees and O is the circumcenter of the circle.
1. Identify the Given Information:
- We know that O is the circumcenter of triangle ABC.
- Angle OBC = 37 degrees.
2. Understand the Properties of the Circumcenter:
- Since O is the circumcenter, OA, OB, and OC are all radii of the circumcircle. Therefore, OB = OC = OA.
3. Use the Isosceles Triangle Property:
- In triangle OBC, since OB = OC, the angles opposite to these sides are equal. Thus, angle OCB = angle OBC = 37 degrees.
4. Calculate Angle BOC:
- The sum of angles in triangle OBC is 180 degrees. Therefore:
Angle BOC+Angle OBC+Angle OCB=180∘
Angle BOC+37∘+37∘=180∘
Angle BOC+74∘=180∘
Angle BOC=180∘−74∘=106∘
5. Relate Angle BOC to Angle BAC:
- According to the property of circles, the angle at the center (angle BOC) is twice the angle at the circumference (angle BAC) that subtends the same arc. Therefore:
Angle BOC=2×Angle BAC
106∘=2×Angle BAC
6. Solve for Angle BAC:
- Dividing both sides by 2 gives:
Angle BAC=106∘2=53∘
Final Answer:
- Angle BAC = 53 degrees.
- We know that O is the circumcenter of triangle ABC.
- Angle OBC = 37 degrees.
- Since O is the circumcenter, OA, OB, and OC are all radii of the circumcircle. Therefore, OB = OC = OA.
- In triangle OBC, since OB = OC, the angles opposite to these sides are equal. Thus, angle OCB = angle OBC = 37 degrees.
- The sum of angles in triangle OBC is 180 degrees. Therefore:
Angle BOC+Angle OBC+Angle OCB=180∘
Angle BOC+37∘+37∘=180∘
Angle BOC+74∘=180∘
Angle BOC=180∘−74∘=106∘
- According to the property of circles, the angle at the center (angle BOC) is twice the angle at the circumference (angle BAC) that subtends the same arc. Therefore:
Angle BOC=2×Angle BAC
106∘=2×Angle BAC
- Dividing both sides by 2 gives:
Angle BAC=106∘2=53∘
- Angle BAC = 53 degrees.
Topper's Solved these Questions
Similar Questions
Knowledge Check
O is the circumcentre of the △ABC. If ∠BAC=50∘, then ∠OBC is equal to
A30∘B60∘C40∘D50∘O is the centre of a circle ∠AOB=90∘and∠BOC=120∘.∠ABC is equal to
 A150∘B210∘C75∘D105∘
A150∘B210∘C75∘D105∘In the figure, O is the centre of the circle . ∠PQR is equal to
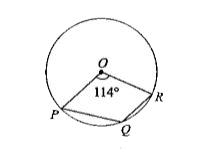 A57∘B63∘C123∘D92∘
A57∘B63∘C123∘D92∘
In the figure, O is centre of a circle. If ∠BAC=20∘and∠ACB=30∘. Find ∠AOC
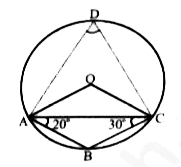
View SolutionIf O is the circumcentre of a triangle ABC lying inside the tri angle, then ∠OBC+∠BAC is equal to
View SolutionIn a ΔABC, O is its circumcentre and ∠BAC=50∘. The measure of ∠OBC is
View SolutionIf O is the incentre of a triangle ABC and ∠AOC=124∘, find the ∠ABC.
View SolutionIn a circle with the centre is O and AB is the diameter of the circle and CD is the chord of the circle. If angle ABC is 54∘ and the length of CD and BC is equal, then find the ∠DBC.
View Solution

