Can two numbers have 15 as their H.C.F. and 110 as their L.C.M.? Give reason to justify your answer.
The correct Answer is:No; LCM of two numbers is always divisible by their HCF
To determine whether two numbers can have 15 as their H.C.F. (Highest Common Factor) and 110 as their L.C.M. (Lowest Common Multiple), we can follow these steps:
Step 1: Understand the relationship between H.C.F. and L.C.M.
The relationship between H.C.F. and L.C.M. of two numbers can be expressed by the formula:
H.C.F.×L.C.M.=Product of the two numbers
This means that the product of the H.C.F. and L.C.M. should equal the product of the two numbers.
Step 2: Substitute the given values into the formula.
Given:
- H.C.F. = 15
- L.C.M. = 110
Using the formula:
15×110=Product of the two numbers
Calculating this gives:
15×110=1650
Step 3: Check if L.C.M. is divisible by H.C.F.
For two numbers to have 15 as their H.C.F. and 110 as their L.C.M., the L.C.M. must be divisible by the H.C.F. This means:
11015
Calculating this gives:
110÷15=7.33(not an integer)
Since 110 is not divisible by 15, this indicates that the condition is not satisfied.
Step 4: Conclusion
Since the L.C.M. (110) is not divisible by the H.C.F. (15), it is not possible for two numbers to have 15 as their H.C.F. and 110 as their L.C.M.
Final Answer
No, two numbers cannot have 15 as their H.C.F. and 110 as their L.C.M. because 110 is not divisible by 15.
---
The relationship between H.C.F. and L.C.M. of two numbers can be expressed by the formula:
H.C.F.×L.C.M.=Product of the two numbers
This means that the product of the H.C.F. and L.C.M. should equal the product of the two numbers.
Given:
- H.C.F. = 15
- L.C.M. = 110
15×110=Product of the two numbers
Calculating this gives:
15×110=1650
For two numbers to have 15 as their H.C.F. and 110 as their L.C.M., the L.C.M. must be divisible by the H.C.F. This means:
11015
Calculating this gives:
110÷15=7.33(not an integer)
Since 110 is not divisible by 15, this indicates that the condition is not satisfied.
Since the L.C.M. (110) is not divisible by the H.C.F. (15), it is not possible for two numbers to have 15 as their H.C.F. and 110 as their L.C.M.
No, two numbers cannot have 15 as their H.C.F. and 110 as their L.C.M. because 110 is not divisible by 15.
Similar Questions
Knowledge Check
- Question 1 - Select One
If H.C.F. of two numbers is 15 and their product is 1575, then their L.C.M. is
A15B105C525D1575
Can two numbers have 18 as their HCF and 380 as their LCM? Give reason.
View SolutionCan two number have 18 as their HCF and 380 as their LCM? Give reason
View SolutionCan two numbers has 16 as H.C.F. and 380 as L.C.M .
View SolutionCan two numbers have 12 as their HCF and 512 as their LCM? Justify your answer.
View SolutionConsider the following circuit :
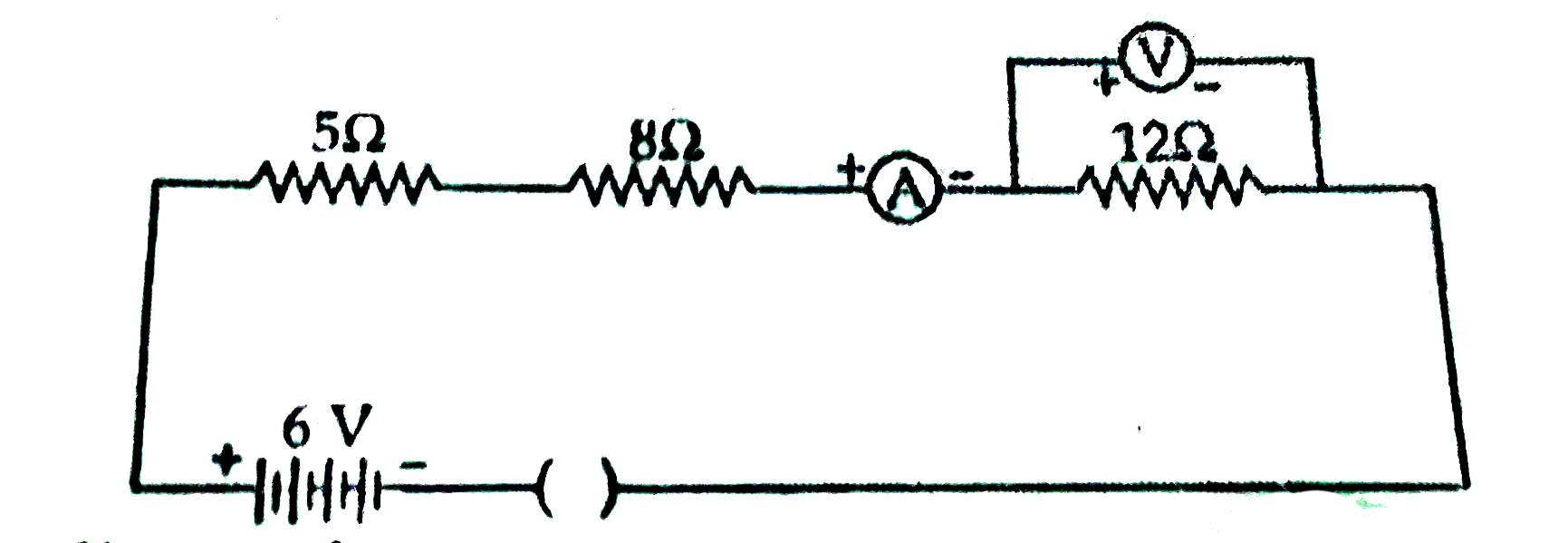
What would be the readings of the ammeter and the voltmeter when key is closed ? Give reason to justify your answers .View SolutionA gas cylinder can hold 1 kg of hydrogen gas at room temperature and 1 atm pressure. Calculate the following:
The number of molecules of carbon dioxide in the cylinder. Give reasons to justify your answer. Mass of the substanceView SolutionAnswer the following:
(i) Obtain the expression for the cyclotron frequency.
(ii) A deuteron and a proton are accelerated by the cyclotron. Can both be accelerated with the same oscillator frequency ? Give reason to justify your answer.View Solution
