Question

${\int }_0^{x^2}\frac{t^2-5t+4}{2+e^t}dt$ के उच्चिष्ठ या निम्निष्ठ के बिन्दु ज्ञात कीजिए।

Answer

` - 2, 0, 2 `

Explanation

माना `f(x)=int _( 0) ^( x^(2)) ( t^(2) - 5 t + 4)/( 2 + e^(t)) dt`

न्यूटन लेबनीज़ नियम से -

`d/(dx)int_(g(x))^(h(x))f(t)dt`

`" "=f`[`h(x)`]`.h'(x)`

`" "-f`[`g(x)`]`.g'(x)`

`f'(x)=( x^(4) - 5 x^2 + 4)/( 2 + e^(x^2))2x-0`

`=((x-1)(x+1)(x-2)(x+2)2x)/(2 + e^(x^2))`

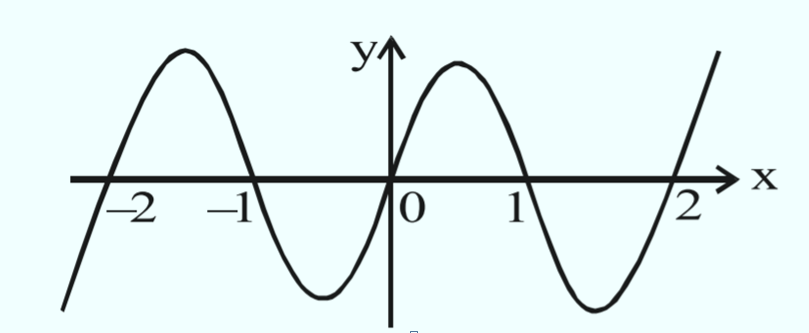
वक्र `"(wavy curve)"` से यह ज्ञात होता है कि `f '(x )` अपने चिह्न `x=pm2, pm1,0` पर बदलता है अर्थात `-1,1` उच्चिष्ठ के बिन्दु हैं तथा `-2,0,2` निम्निष्ठ बिन्दु हैं।