Find the sum of the first n terms of the arithmetic sequence
1n,3n,5n,7n,.......Solution in Malayalam
Step by step video & image solution for Find the sum of the first n terms of the arithmetic sequence1/n,3/n,5/n,7/n,....... by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure O is the centre of circle. □AOC=80o
What is the measure of □ABC?
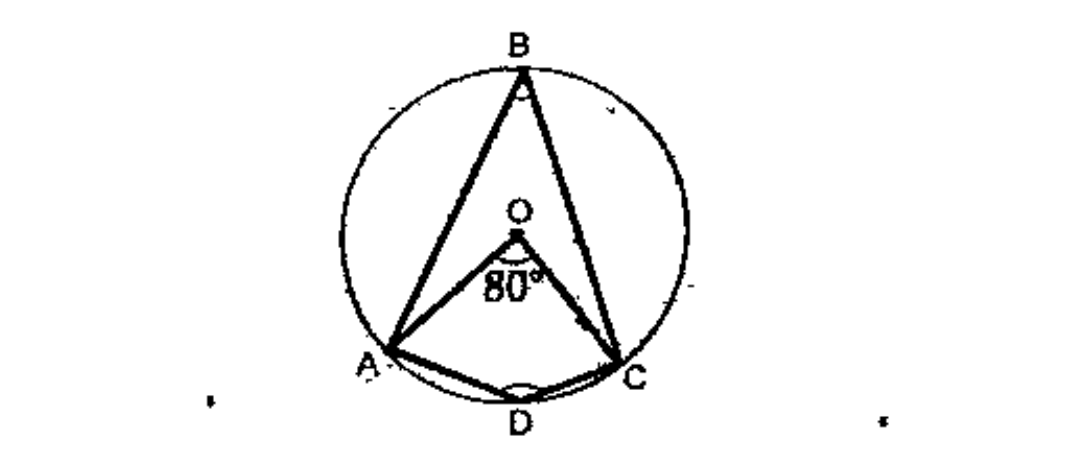 .
.
View SolutionIf the sum of n terms of sequence S_(n)=(n)/(n+1)
View SolutionFind the sum of n terms of the sequence (an),wherean=5−6n,n∈N.
View SolutionFind the sum of n terms of the arithmetic-geometric sequence.
View SolutionFind the sum of n terms of the sequence given by an=(3n+5n),n∈N.
View SolutionIf the sum of the first n terms of a sequence is 2(7n−1)/3 show that it is a G.P. Also , find its first term and common ratio.
View SolutionLet S be the sum of the first n terms of the arithmetic sequence 3, 7, 11, ...., and let T be the sum of the first n terms of the arithmetic sequence 8 , 10 , 12 ,.... For n > 1 , S = T for
View SolutionIf the sum of the first n terms of a sequence is equal to √(32)(n2−n) , then the sum of the squares of these terms is equal to
View SolutionIf nth term of the sequences isan=(−1)n−15n+1 , Find a3 ?
View SolutionThe sum of first 'n' terms of an arithmetic progression is 210 and sum of its first (n-1) terms is 171. If the first term 3, then write the arithmetic progression.
View Solutionयदि an=n3−n2+5n−1n+1 तब अनुक्रम के प्रथम चार पद ज्ञात कीजिए।
View SolutionIf the sum of first n terms of an arithemetic progression 2,5,8… is equal to sum of the first n terms of another arithmetic progression 57,59,61.. Then find the value of n
View Solutionयदि किसी श्रेणी के प्रथम n पदों का समान्तर माध्य x है तथा प्रथम (n-1) पदों का योग k है, तो उसका nवाँ पद है
View SolutionThe sum of first n terms of an arithmetic sequence is n2+2n What is the first term?
View SolutionThe sum of first n terms of an arithmetic sequence is n2+2n Find the common difference.
View Solution
