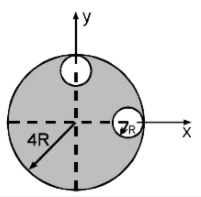
4R त्रिज्या की वृत्ताकार चकती से, R त्रिज्या की दो चकतियाँ काटी गई हैं नयी संचरना का द्रव्यमान केन्द्र होगा - (निचली वृत्ताकार गुहिका (cavity) का केन्द्र x-अक्ष पर स्थित है तथा ऊपरी वृत्ताकार गुहिका (cavity) का केन्द्र y-अक्ष पर स्थित है।)
ˆiR5+ˆjR5
−ˆiR5+ˆjR5
−ˆiR5−ˆjR5
−3R14(ˆi+ˆj)
The correct Answer is:D
4R त्रिज्या की वत्ताकार चकती का द्रव्यमान केन्द्र =(0,0)
ऊपरी चकती का द्रव्यमान केन्द्र = (0,3R)
निचली चकती का द्रव्यमान केन्द्र =(3R,0)
माना M पूरी चकती का द्रव्यमान हैं। तो काटी गई चकतियों के द्रव्यमान M16 होंगे। इसलिये नई संरचना का द्रव्यमान केन्द्र हैं -
¯x=m1x1−m2x2−m3x3m1−m2−m3=M(0)−M16(0)−M16(3R)M−M16−M16=−3R14
¯y=m1y1−m2y2−m3y3m1−m2−m3=M(0)−M16(3R)−M16(0)M−M16−M16=−3R14
द्रव्यमान के केन्द्र का स्थिति सदित =−3R14(ˆi+ˆj)
Topper's Solved these Questions
Similar Questions
एक वस्तु पर समय के साथ परिवर्ती बल →F=(3ˆi+5ˆj)N लग रहा है जिसके कारण इसकी स्तिथि समय के साथ →s=(2t2ˆi−5ˆj) की तरह बदलती है यहाँ t सेकंड में है इस बात द्वारा प्रारंभिक 2s में किया गया कार्य होगा-
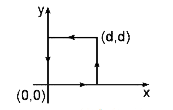
View Solutionबल →F=A(y2ˆi+2x2ˆj) द्वारा दर्शाये गये पथ में किया गया कार्य, जहाँ A एक नियतांक है और x व y मीटर में हैं :
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसकी x-अक्ष से दूरी उसकी y-अक्ष से दूरी की तीन गुनी है ।
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View SolutionY-अक्ष पर केन्द्र (centre) और त्रिज्या (radius) 4 वलए वृत्तों (circels) के कुल (family) को निरूपित करने वाला अवकलन समीकरण (differential equations) है
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View Solutionयदि किसी गोले का समीकरण x2+y2+z2+2ux+2vy+2wz+d=0 है, तो गोले के केन्द्र का निर्देशांक तथा त्रिज्या क्या होगी?
View Solutionउस गोले का सदिश समीकरण ज्ञात कीजिए जिसका केन्द्र (2,-3,4) तथा त्रिज्या 5 है।
View Solutionउस गोले का सदिश समीकरण ज्ञात कीजिए जिसका केन्द्र (ˆi+2ˆj−3ˆk) तथा त्रिज्या 5 है।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जिसका केन्द्र (2, 2, 1 ) तथा त्रिज्या 4 है।
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष तथा केन्द्र पर चुंबकीय क्षेत्र | ऐम्पियर का परिपथीय नियम
View Solution
