दो कण जिनके द्रव्यमान 10kg तथा 30kg हैं औन उनके स्थिति सदित क्रमश: ˆi+ˆj+ˆk तथा −ˆi−ˆj−ˆk हैं तो इनके द्रव्यमान केन्द्र की स्थिति होगी -
a. −(ˆi+ˆj+ˆk)2
b. (ˆi+ˆj+ˆk)2
c. −(ˆi+ˆj+ˆk)4
d. (ˆi+ˆj+ˆk)4
The correct Answer is:(A)
RCM=m1→r1+m2→r2m1+m2
RCM=−(ˆi+ˆj+ˆk)2
Topper's Solved these Questions
Similar Questions
वत्ताकार पथ में चलने वाले कण के रेखिक वेग, उसके स्थिति सदि । व कोणीय वेग में सम्बन्ध होता है|
View Solutionएक कण पर कार्यरत बल के घटक प्रदर्शित ग्राफ के अनुसार परिवर्तित होते है। जब कण (0,5,12) से (4,20,0) तक चलता है तब इस बल द्वारा किया गया कार्य है :
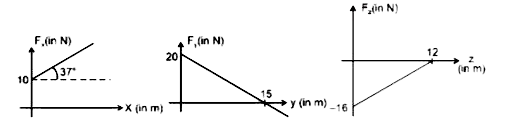
View SolutionWrite the value of ˆi.(ˆj׈k)+ˆj.(ˆi׈k)+ˆk.(ˆi׈j).
View Solutionयदि ˆi,ˆj,ˆk क्रमशः X,Y,Z अक्ष की दिशा में एकांक सदिश हो तो सिद्ध कीजिये -
(a) ˆi⋅ˆi=ˆj⋅ˆj=ˆk⋅ˆk=1
(b) ˆi⋅ˆj=ˆi⋅ˆk=ˆj⋅ˆk=0
(c) ˆi׈i=ˆj׈j=ˆk׈k=0
View Solutionˆi⋅(ˆj׈k)+ˆj⋅(ˆk׈i)+ˆk⋅(ˆi׈j)=
View Solution[ˆiˆjˆk]+[ˆkˆjˆi]+[ˆjˆkˆi]=
View Solution[ˆi ˆj ˆk]=[ˆj ˆk ˆi]=[ˆk ˆi ˆj] का मान होगा -
View Solutionसमान्तर रेखाओं ¯r=(ˆi+2ˆj+3ˆk)+λ(ˆi−ˆj+ˆk)तथा¯r=(2ˆi−ˆj−ˆk)+μ(ˆi−ˆj+ˆk) के मध्य की न्यूनतम दूरी ज्ञात कीजिए ।
View Solutionरेखाओं →γ=(ˆi+2ˆj+ˆk)+λ(ˆi−ˆj+ˆk) तथा →γ=(2ˆi−ˆj−ˆk)+μ(2ˆi+ˆj+2ˆk) के बीच की लघुत्तम दूरी ज्ञात कीजिए ।
View Solutionμ के उन भिन्न वास्तविक मानो का योग, जिनके लिए सदिश μˆi+ˆj+ˆk,ˆi+μˆj+ˆk तथा ˆi+ˆj+μˆk समतलीय (co-planar) है, है
View Solutionबिन्दु, जिनके स्थिति सदिश 60ˆi+3ˆj,40ˆi−8ˆj तथा aˆi−52ˆj हैं, सरेखीय होंगे। यदि
View Solutionλ का मान, यदि सदिश ˆi−3ˆj+ˆk,2ˆi+λˆj+ˆk तथा 3ˆi+ˆj−2ˆk एक समतल में हों, होगा
View SolutionIf the vectors ˆi−ˆj,ˆj+ˆkand→a form a triangle, then →a may be a. −ˆi−ˆk b. ˆi−2ˆj−ˆk c. 2ˆi+ˆj+ˆk d. ˆi+ˆk
View SolutionEvaluate : [ˆiˆjˆk]+[ˆjˆkˆi]+[ˆkˆiˆj] [2ˆiˆjˆk]+[ˆiˆkˆj]+[ˆkˆj2ˆi]
View SolutionEvaluate the following: [ˆi ˆj ˆk]+[ˆj ˆk ˆi]+[ˆk ˆi ˆj] .
View Solution
