कथन-1 यदि एक त्रिभुज की bhujaayen x,y,z इस प्रकार है की x+y+z=1
तो (2x−1+2y−1+2z−13)≥((2x−1)(2y−1)(2z−1))1/3
कथन -2 धनात्मक संख्याओं A.M≥G.M≥H.M.
कथन -1 सत्य है , कथन -2 कथन -1 का ही स्पष्टीकरण है।
कथन -1 सत्य है , कथन -2 कथन -1 का ही स्पष्टीकरण नहीं है।
कथन -1 सत्य है , कथन-2 असत्य है।
कथन -1 असत्य है , कथन-2 सत्य है।
The correct Answer is:D
Step by step video, text & image solution for कथन-1 यदि एक त्रिभुज की bhujaayen x,y, z इस प्रकार है की x+ y + z =1 तो ((2x-1+2y - 1 +2z- 1)/( 3)) ge ( (2x- 1) (2y -1) ( 2z- 1))^(1//3) कथन -2 धनात्मक संख्याओं A.Mge G.M ge H.M. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
AB के लंबवत ED है , AB = 20 इकाई तथा AC=12 इकाई है।
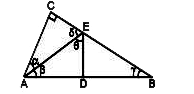
त्रिभुज AEC का क्षेत्रफल है-
View Solutionअंतराल [0,5π] में समीकरण 3sin2x−7sinx+2=0 के हेलो की संख्या होगी
View SolutionIf x(2x+y+z)=y(x+2y+z)=z(x+y+2z)=a , then find a if x+y+z≠0 . (a)13 (b) 14 (c) 12 (d) 18
View SolutionIf x+y+z=xzy, prove that : 2x1−x2+2y1−y2+2z1−z2=2x1−x22y1−y22z1−z2
View SolutionIf x+y+z=xyz, prove by trignometry that:
2x1−x2+2y1−y2+2z1−z2=2x1−x2.2y1−y2.2z1−z2
View SolutionIf x,y,z > 0 and x + y + z = 1, the prove that
2x1−x+2y1−y+2z1−z≥3.
View SolutionIf x + y + z = xyz, then prove that 2x1−x2+2y1−y2+2z1−z2=2x1−x2⋅2y1−y2⋅2z1−z2.
View Solutionइन समीकरण को क्रेमर नियम से हल कीजिए- x+2y−z=3
3x−y+2z=1
2x−2y+2z=2
View SolutionIf positive numbers x, y, z satisfy x+y+z=1 then
Statement 1: [(1−2x)+(1−2y)+(1−2z)3]≥((1−2x)(1−2y)(1−2z))1/3
because
Statement 2: For any three positive numbers a, b, c their A.M.≥G.M.
View Solutionযদি log(x+y+z)=logx+logy+logz হয়, তবে প্রমাণ করো যে, log(2x1−x2+2y1−y2+2z1−z2)=log(2x1−x2)+log(2y1−y2)+log(2z1−z2)
View Solutionx+y+z=xyz 2x1−x2+2y1−y2+2z1−z2=2x1−x2,2y1−y2,2z1−z2என நிறுவுக
View SolutionIf x+y+z=xyz prove that 2x1−x2+2y1−y2+2z1−z2=2x1−x22y1−y22z1−z2.
View SolutionIf x,y,z > 0 and x + y + z = 1, the prove that
2x1−x+2y1−y+2z1−z≥3.
View SolutionFind all positive real numbers x, y, z such that:
2x−2y+1z=12014,2y−2z+1x=12014,2z−2x+1y=12014
View SolutionFind all positive real numbers x, y, z such that:
2x−2y+1z=12014,2y−2z+1x=12014,2z−2x+1y=12014
View Solution