Let A0A1A2A3A4A5 be a regular hexagon inscribed in acircle of unit radius. Then the product of the length of the line segments A0A1,A0A2andA0A4 is Solution in Telugu
3/4
3√3
3
3√32
The correct Answer is:A
Step by step video, text & image solution for Let A_(0)A_(1)A_(2)A_(3)A_(4)A_(5) be a regular hexagon inscribed in acircle of unit radius. Then the product of the length of the line segments A_(0)A_(1),A_(0)A_(2)andA_(0)A_(4) is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBook:AAKASH SERIESChapter:PROPERTIES OF TRIANGLESExercise:PRACTICE SHEET (EXERCISE-IV) (LEVEL-II) (Matrix Matching Type Questions)
Explore 2 Videos
- PROPERTIES OF TRIANGLESBook:AAKASH SERIESChapter:PROPERTIES OF TRIANGLESExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL 1 (MAIN)) (Straight Objective Type Questions)
Explore 59 Videos
- PROPERTIES OF TRIANGLESBook:AAKASH SERIESChapter:PROPERTIES OF TRIANGLESExercise:PRACTICE SHEET (EXERCISE-IV) (LEVEL-I) (Straight Objective Type Questions)
Explore 4 Videos
- PLANESBook:AAKASH SERIESChapter:PLANESExercise:ADVANCED SUBJECTIVE TYPE QUESTIONS
Explore 30 Videos
- PROPERTIES OF VECTORSBook:AAKASH SERIESChapter:PROPERTIES OF VECTORSExercise:PRACTICE EXERCISES
Explore 55 Videos
Similar Questions
Let O be the circumcentre, H be the orthocentre, I be the incentre and I1I2,I3 be the excentres of acuteangled ΔABC
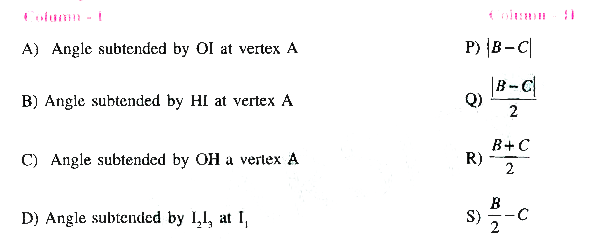
View SolutionIn a right-angled isosceles triangle, the ratio of the circumradius and inradius is
View SolutionIf h, k are the perpendicular distances from (4, 2, 5) to the x-axis, y-axis respectively, then hk =
View SolutionThe plane 2x + 3y + kz - 7 = 0 is parallel to the line whose d.r's are (2,-3,1) then k=
View SolutionIf ¯¯¯¯¯¯OA=¯i+2¯j−3¯k,¯¯¯¯¯¯OB=3¯i−2¯j+5¯kand2¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB then ¯¯¯¯¯¯AC=
View SolutionA_(0),A_(1),A_(2),A_(3),A_(4),A_(5) be a regular hexagon inscribed in a circle of unit radius,then the product of (A_(0)A_(1)*A_(0)A_(2)*A_(0)A_(4) is equal to
View SolutionLet A_(0)A_(1)A_(2)A_(3)A_(4)A_(5) be a regular hexagon inscribed in a circle of unit radius.Then the product of the lengths the line segments A_(0)A_(1),A_(0)A_(2) and A_(0)A_(4) is
View SolutionIf a_(1),a_(2)...a_(n) are the first n terms of an Ap with a_(1)=0 and d!=0 then (a_(3)-a_(2))/(a_(2))+(a_(4)-a_(2))/(a_(3))+(a_(5)-a_(2))/(a_(4))...+(a_(n)-a_(2))/(a_(n-1)) is
View SolutionIf (1+x)2n=a0+a1x+a2x2+…+a2nx2n, then
(a0−a2+a4−a6+…−a2n)2+(a1−a3+a5−a7+...+a2n−1)2 is equal to
View SolutionLet a1,a2,a3,a4anda5 be such that a1,a2anda3 are in A.P., a2,a3anda4 are in G.P., and a3,a4anda5 are in H.P. Then, a1,a3anda5 are in
View Solutionif (1+ax+bx2)4=a0+a1x+a2x2+…..+a8x8, where a,b,a0,a1…….,a8∈R such that a0+a1+a2≠0 and
∣∣ ∣∣a0a1a2a1a2a0a2a0a1∣∣ ∣∣=0 then the value of 5.ab is ____
View Solutionयदि (1+ax+bx2)4=a0+a1x+a2x2+....+a8x8, जहाँ a,b,a0,a1,...A(8)∈R,a,b!=0, इस प्रकार है कि
a0+a1+a2≠0 तथा ∣∣ ∣∣a0a1a2a1a2a0a2a0a1∣∣ ∣∣=0
a का मान होगा
View Solutionयदि (1+ax+bx2)4=a0+a1x+a2x2+....+a8x8, जहाँ a,b,a0,a1,...A(8)∈R,a,b!=0, इस प्रकार है कि
a0+a1+a2≠0 तथा ∣∣ ∣∣a0a1a2a1a2a0a2a0a1∣∣ ∣∣=0
b का मान होगा
View Solutionमाना A0,A1,A2,A3,A4,A5 किसी इकाई त्रिज्या के वृत्त के भीतर बनने वाले समषटभुज के शीर्ष हों, तो रेखाखण्डों A0A1,A0A2 तथा A0A4 की लम्बाईयो का गुणनफल होगा
View SolutionLet A_(0)A_(1)A_(2)A_(3)A_(4)A_(5) be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the segments A_(0)A_(1) , A_(0)A_(2) and A_(0)A_(4) is
View SolutionLet A0,A1,A2,A3,A4 and A5 be the consecutive vertices of a regular hexagon inscribed in a circle of radius 1 unit. Then the product of the lengths of A0A1, A0A2 and A0A4 is
View Solution

