एक समतल निर्देशी अक्षों को A, B, C पर इस प्रकार मिलता है, कि △ABC का केन्द्रक बिन्दु (p, q, r) है। प्रदर्शित कीजिए कि समतल का समीकरण xp+yq+zr=3 होगी।
The correct Answer is:3
Step by step video, text & image solution for एक समतल निर्देशी अक्षों को A, B, C पर इस प्रकार मिलता है, कि triangleABC का केन्द्रक बिन्दु (p, q, r) है। प्रदर्शित कीजिए कि समतल का समीकरण x/p + y/q + z/r=3 होगी। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - DO YOURSELF-1
5 Videos
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - DO YOURSELF-2
3 Videos
- AREA UNDER THE CURVEBOOK - ALLEN HINDICHAPTER - AREA UNDER THE CURVEEXERCISE - Exercise-05 [B]
21 Videos
Similar Questions
बिन्दु P(3, 4, 5) तथा Q(-1, 2, -3) के मध्य दूरी ज्ञात कीजिए।
View Solutionमूल बिन्दु O को बिन्दु P(3, 2, -5) से जोड़ने वाले रेखा खण्ड का अक्षों पर प्रक्षेप ज्ञात कीजिए।
View Solutionवक्र f(x)=x2+bx−b के बिन्दु (1,1) पर स्पर्श रेखा तथा निर्देशी अक्षो से बना त्रिभुज प्रथम चतुर्थांश में स्थित है | यदि इसका क्षेत्रफल 2 है, तो b का मान है -
View Solutionबिन्दुओ (4,-1,2) और (-3,2,3) को मिलाने वाली रेखा एक समतल को बिंदु (-10,5,4) पर लंबवत मिलती है समतल का समीकरण ज्ञात कीजिये
View Solutionबिन्दु (1,0,0) से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो XZ-समतल पर लम्ब है।
View Solutionबिन्दु (−3,5,2) का समतल 2x−y+z=0 पर प्रतिबिम्ब ज्ञात कीजिए।
View Solutionदी गई आकृति में △ABC का बहिर्वृत्त भुजाओ को Q ,P एवं R पर स्पर्श करता है। यदि AQ=8 सेमी हो तो △ABC का परिमाप ज्ञात कीजिए।
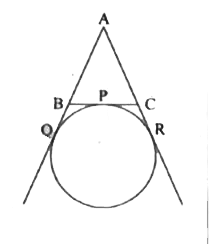
View Solutionउस समतल का समीकरण ज्ञात कीजिए जो X, Y और Z-अक्षों पर क्रमशः 1, 2 और 3 अन्तःखण्ड काटता है |
View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionयदि बिन्दु P(−3,4) से होकर जाने वाली एक सरल रेखा इस प्रकार है कि इसके निर्देशांक अक्षो के बीच अंत: खंडित भाग का मध्य -बिन्दु P है, तो इसका समीकरण है
View Solutionरेखा x−6−1=y+10=z+34 तथा समतल x+y-z=3 का प्रतिच्छेद बिन्दु है
View Solution
