माना H1,H2,….,Hn परस्पर अपवर्जी तथा निःशेष घटना , P(Hi)>0,i=1,2,…,n के साथ है। माना E एक दूसरी घटना 0<P(E)<1 के साथ है।
कथन-I : P(Hi∣E)>P(E∣Hi),P(Hi),i=1,2,…,n के लिए
क्योंकि
कथन-II : n∑i−1P(Hi)=1
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है।
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
कथन-I, सत्य है परन्तु कथन -II असत्य है।
कथन-I, असत्य है परन्तु कथन -II सत्य है।
The correct Answer is:D
Step by step video, text & image solution for माना H_(1), H_(2),….,H_(n) परस्पर अपवर्जी तथा निःशेष घटना , P(H_(i)) gt 0, i = 1,2,…,n के साथ है। माना E एक दूसरी घटना 0 lt P (E) lt 1 के साथ है। कथन-I : P(H_(i)|E) gt P(E|H_(i)), P(H_(i)), i= 1, 2,…,n के लिए क्योंकि कथन-II : sum_(i-1)^(n) P(H_(i)) = 1 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - PROBABILITYEXERCISE - Exercise-05 [A] JEE-[MAIN] Previous Year Questions22videos
PROBABILITY
- BOOK - ALLEN HINDICHAPTER - PARABOLA EXERCISE - DO YOURSELF - 72videos
PARABOLA
- BOOK - ALLEN HINDICHAPTER - TANGENT & NORMAL EXERCISE - EXERCISE -05 (B) JEE-(ADVANCED) : PREVIOUS YEAR QUESTIONS5videos
TANGENT & NORMAL
Similar Questions
गणित की एक समस्या हल करने के लिए तीन विद्यार्थियों को दी जाती है, जिनके इसे हल करने की प्रायिकता 12,13,14है, तो प्रायिकता ज्ञात कीजिए कि (i) समस्या हल हो जाती है। (ii) उनमें ठीक एक इसे हल करता है।
05:03View Solutionरेखाओं x=4,y=4 तथा निर्देशी अक्षो से बने वर्गीय क्षेत्र को परवलय y2=4x तथा x2=4y विभाजित करते है। यदि S1,S2,S3 क्रमशः इन भागो के क्षेत्रफल ऊपर से नीचे की ओर अंकित है, तो S1:S2:S3 ज्ञात कीजिए।
07:16View Solutionवक्र y=f(x) के बिन्दु (3,4) पर खींचा गया अभिलम्ब x-अक्ष की धनात्मक दिशा से 3π4 का कोण बनाता है , तो f'(3) बराबर होगा।
06:50View SolutionLet H1,H2,...,Hn be mutually exclusive events with P(Hi)>0,i=1,2,..........n. Let E be any other event with 0<P(E) Statement I P(Hi∣E)>P(E∣Hi.P(Hi) for i=1,2,.......,n statement II n∑i=1P(Hi)=1
View SolutionIf H_(n)=1+(1)/(2)+(1)/(3)+....+(1)/(n),AA n in N then H_(1)+H_(2)+H_(3)+......+H_(n)=
04:33View SolutionSelect the correct answer:
a.
i. PhOC2H5 ii. Ph−−−O−−−Ph
iii. PhI iv. C2H5OC2H5
b.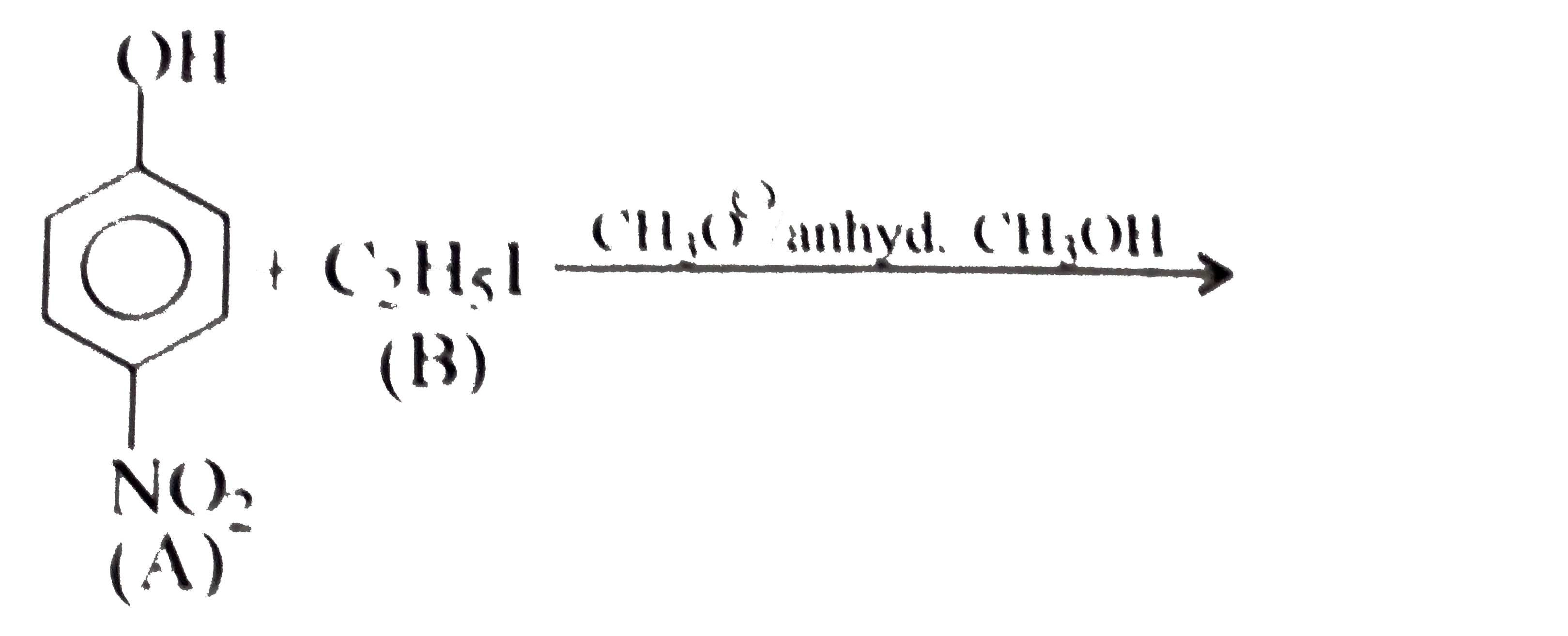
i. p−−NO2−−C6H4−−OC2H5
ii. p−−NO2−−C6H4−−O−−C6H4−−NO2−−p
iii. C2H5−−O−−CH3
iv. p−−NO2−−C6H5−−I.
c.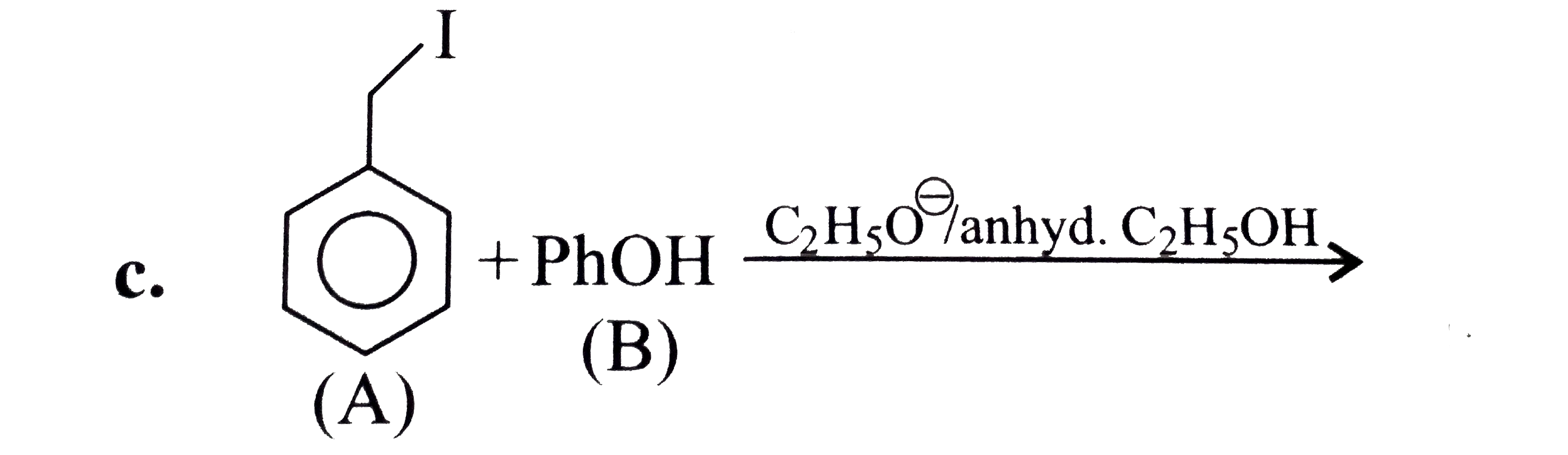
i. C6H5CH2−−O−−Ph
ii. C6H5CH2−−O−−C2H5
iii. Ph−−O−−C2H5
iv. C2H5−−O−−C2H5
d.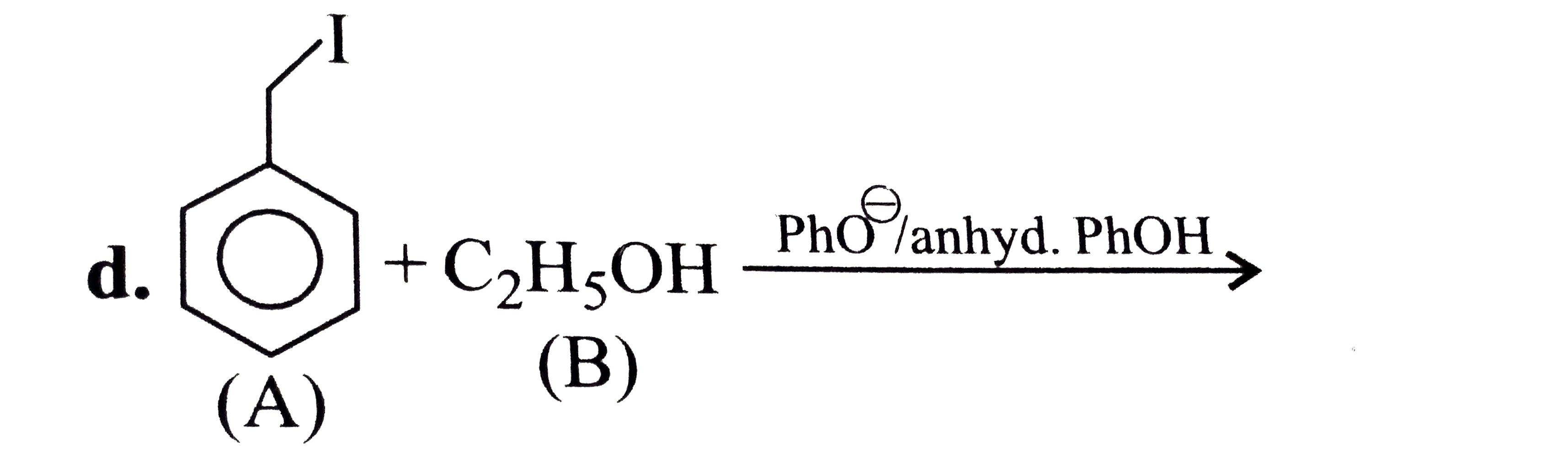
i. C6H5CH2−−O−−C2H5
ii. C6H5−−CH2−−O−−Ph
iii. Ph−−O−−C2H5
iv. C2H5−−O−−C2H5 .
e.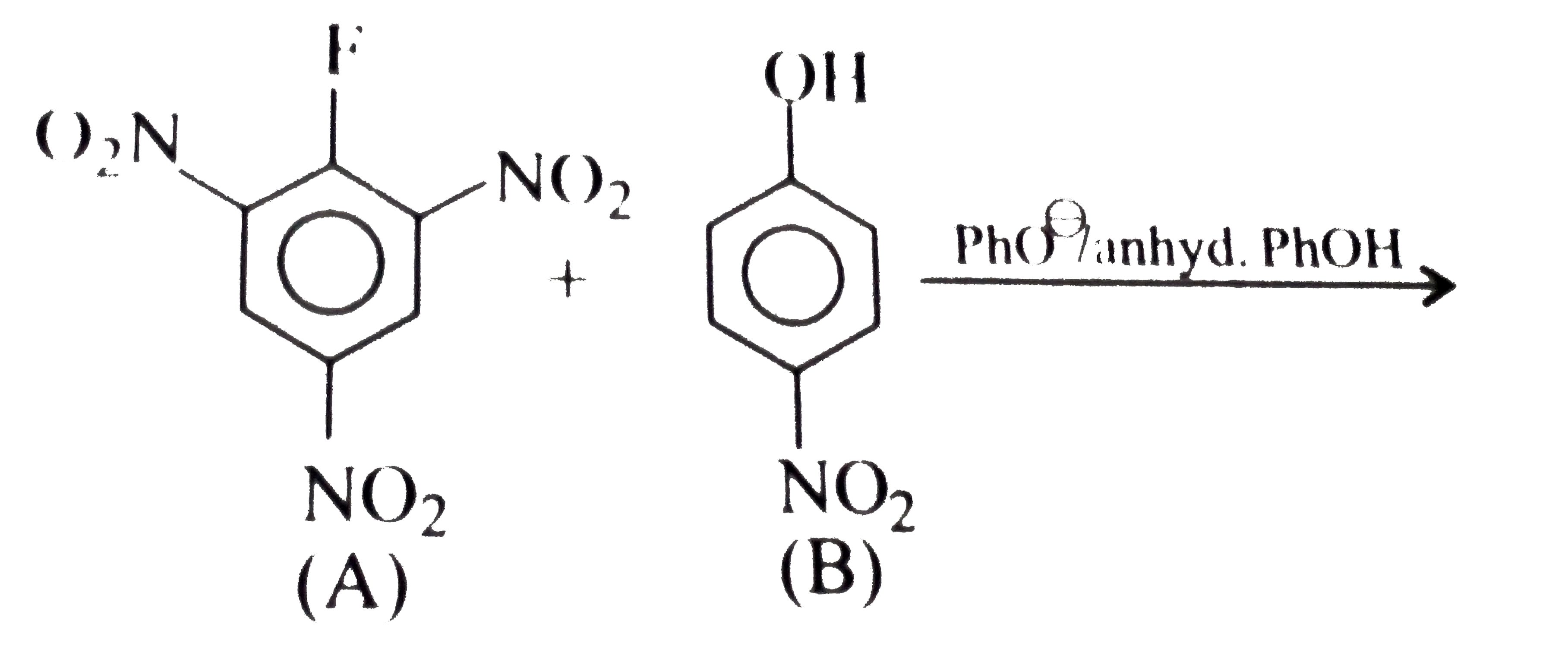
i.
ii.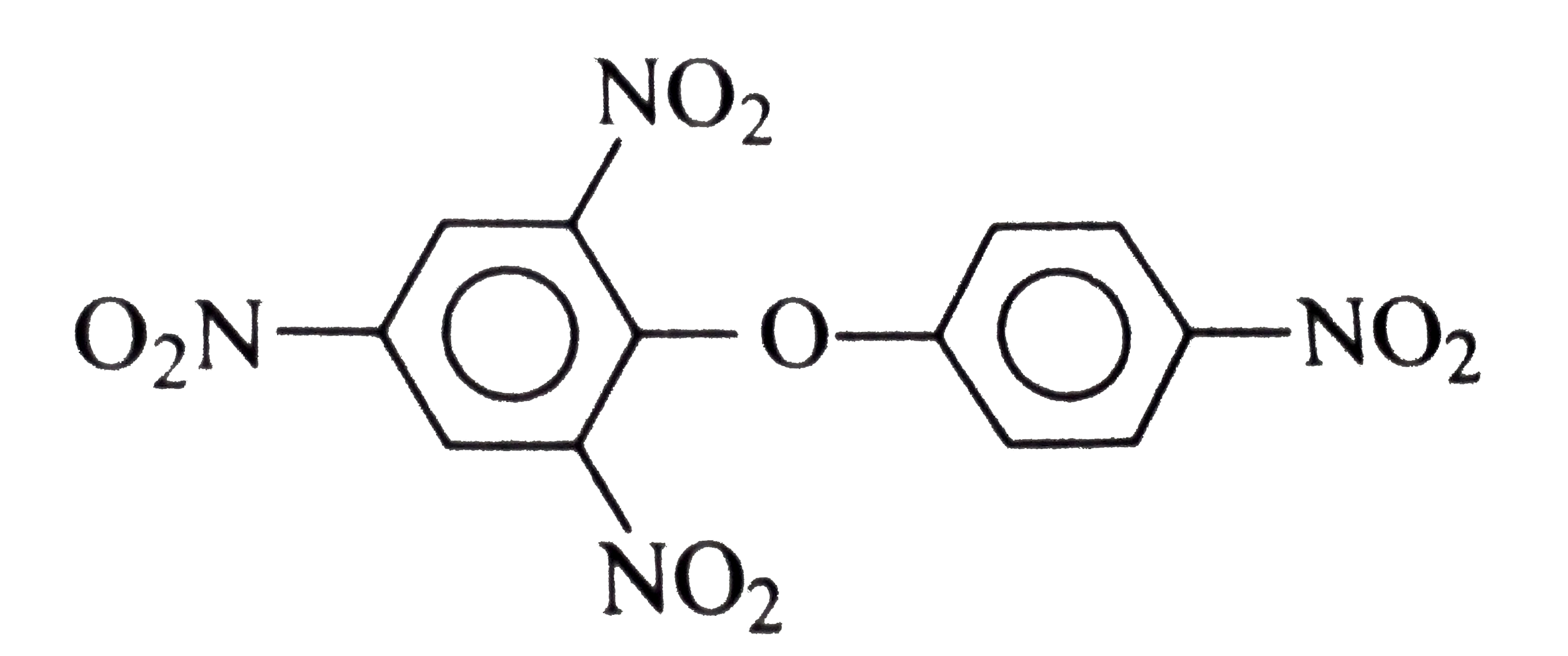
iii.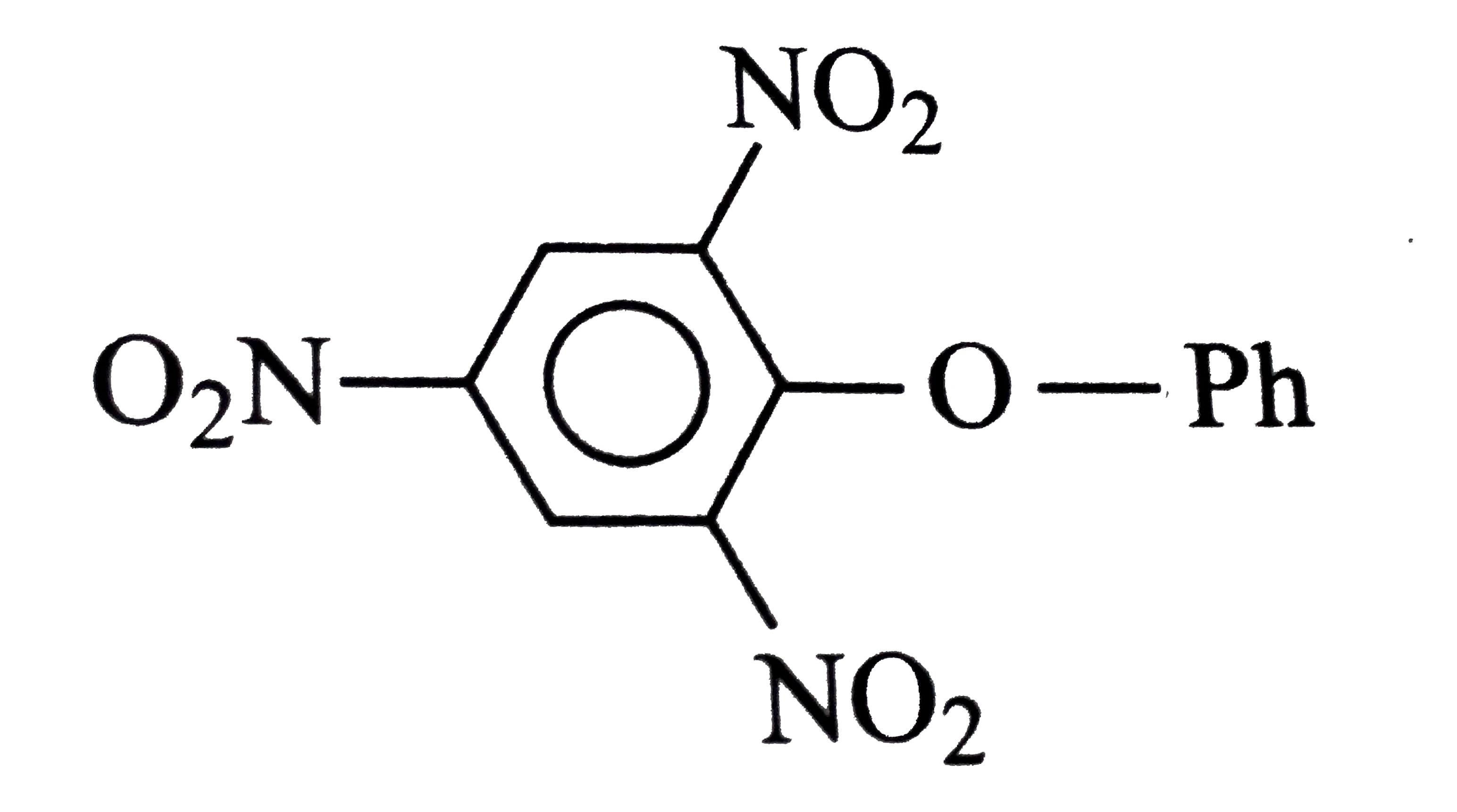
iv.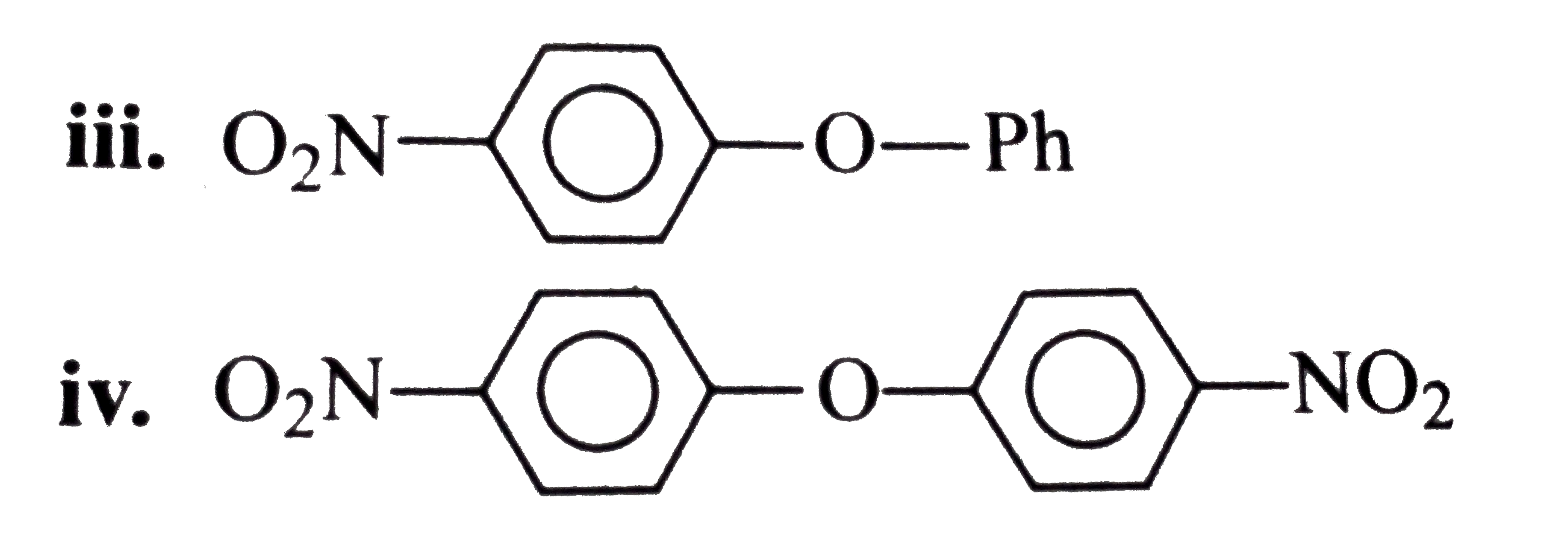
f.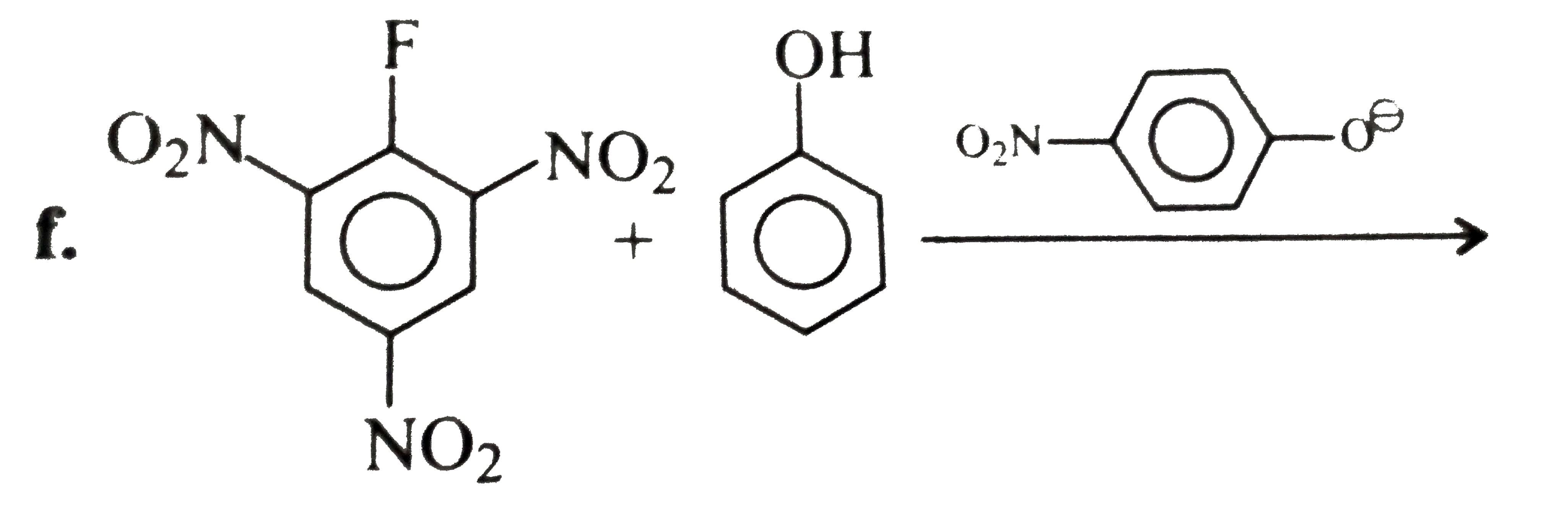
i.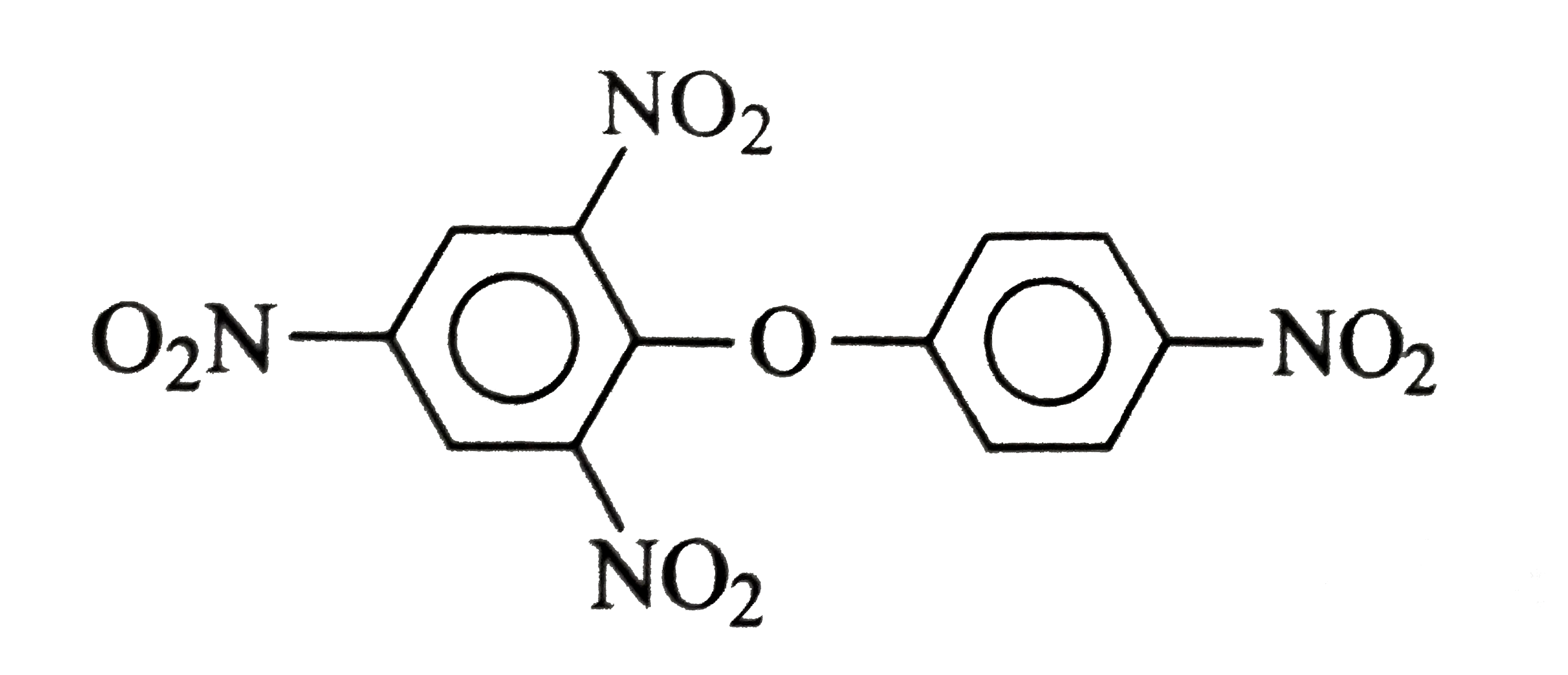
ii.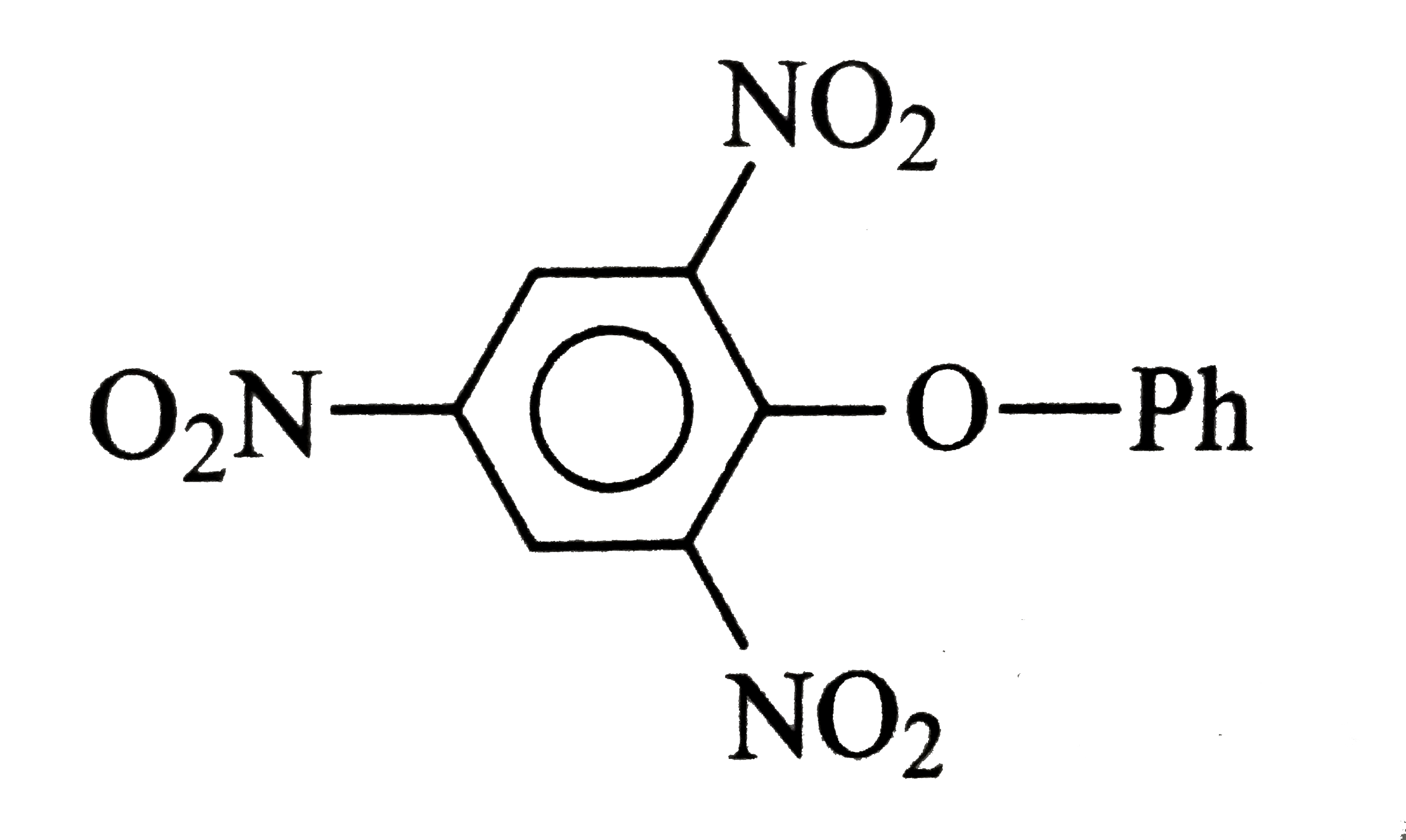
iii.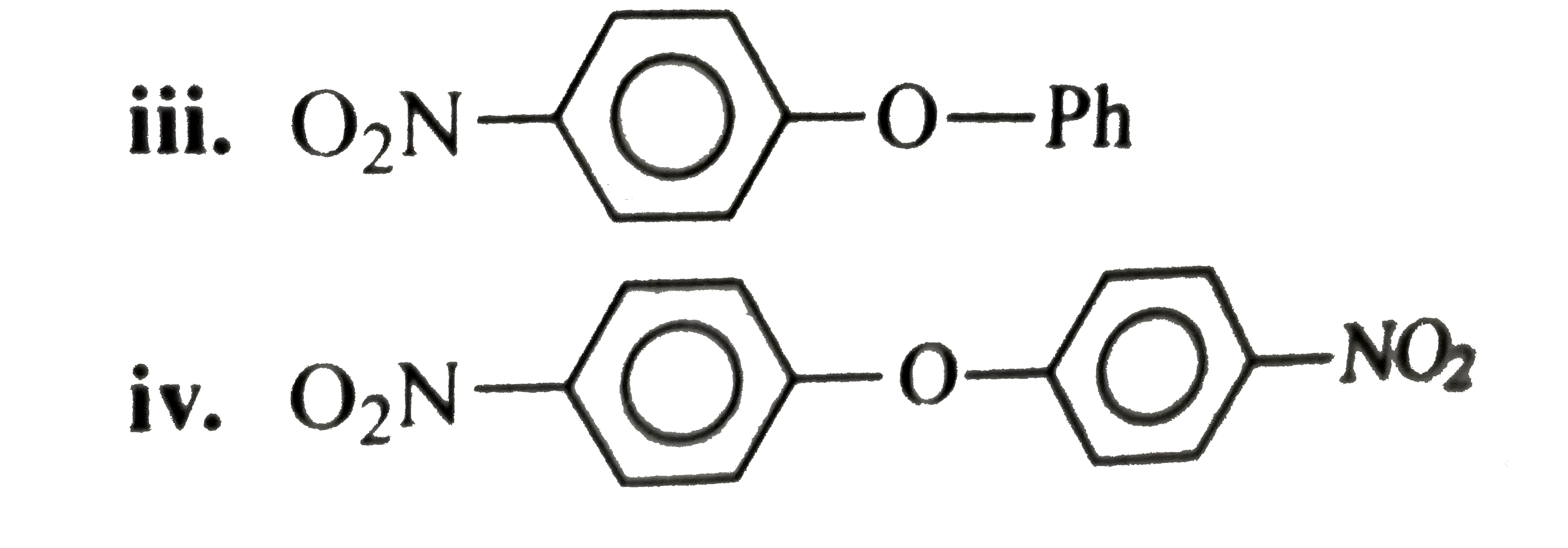
17:06View SolutionGlucose underset((i)(P//HI))overset((i)(HCN//H_(3)O^(oplus)))rarr P P is :
02:21View Solutionमाना कि H1,H2,H3,...,Hn परस्पर अपवर्जी एव सम्पूर्ण n घटनाएँ है, जहाँ P(Hi)>,0i=1,2,3,...,n. मान कि E कोई सुश्री घटना है ताकि 0<P(E)<1.
Statement-1: P(Hi/E)>P(E/Hi).P(Hi),i=1,2,3,...,n.
Statement-2: n∑i=1P(Hi)=1.View Solutionमानाकि w=√3+i2 तथा P={wn:n=1,2,3,..}. इसके अतिरिक्त H1={z∈C:Rez>12} तथा H2={z∈C:Rez<12} , जहाँ C सम्मिश्र संख्याओं का समुच्चय है। यदि z1∈P∩H1,z2∈P∩H2 तथा O मूलबिन्दु प्रदर्शित करता है, तब ∠z1Oz2=
09:34View Solutionमाना H1,H2,….,Hn परस्पर अपवर्जी तथा निःशेष घटना , P(Hi)>0,i=1,2,…,n के साथ है। माना E एक दूसरी घटना 0<P(E)<1 के साथ है।
कथन-I : P(Hi∣E)>P(E∣Hi),P(Hi),i=1,2,…,n के लिए
क्योंकि
कथन-II : n∑i−1P(Hi)=1View SolutionIf H1,H2,H3,…..H2n+1 are in H.P then 2n∑i=1(−1)j(Hi+Hi+1Hi−Hi+1) is equal to
03:33View SolutionFor nonnegative integers s and r , let
(sr)=s!r!(s−r)! 0 if r≤g if >s
For positive integers m and n , let
g(m,n)=m+n∑p=0f(m,n,p)(n+pp)
where for nay nonnegative integer p ,
f(m,n,p)=p∑i=0(n+ii),(n+ip),(p+np−i) Then which of the following statements is/are TRUE ?02:04View SolutionList-I {:((P) H_(2)O gtgt H_(2)S lt H_(2)Se lt H_(2)Te,(1)"Bond angle"),((Q)H_(2)O lt H_(2)S lt H_(2)Se lt H_(2)Te, (2)"melting point and boilinng point"),((R )H_(2)O gt H_(2)S gt H_(2)Se gt H_(2)Te,(3)"acidity"):}
View SolutionThe following compounds are called electrons ( E^(+) ) In order of decreasing relative reactivity to (i) Chlorobenzene, 2-4-dinitrochlorobenzene, p-nitrochlorobenzene (ii) Toluene, p-H_(3)C-C_(6)H_(4)-NO_(2), p-O_(2)N-C_(6)H_(4)-NO_(2)
04:47View Solution{:("COLUMN-I","COLUMN-II"),((A)"Thermal stability",(p)H_(2)Te gt H_(2)Se gt H_(2)S gt H_(2)O),((B)"Acidic nature",(q)H_(2)O gt H_(2)S gt H_(2)Se gt H_(2)Te),((C )"Boiling points",(r )H_(2)S lt H_(2)Se lt H_(2)Te lt H_(2)O),((D) angleM MH " Bond angle",(s) H_(2)S gt H_(2)Se gt H_(2)Te=H_(2)Po):}
04:14View Solution