दिए गये चित्र में दो फलन तथा एक दुसरे को बिन्दु तथा पर काटते है | वक्र तथा का x=0 तथा के मध्य क्षेत्रफल, तथा के मध्य, तथा के मध्य, है| यदि तो फलन ज्ञात कीजिए तथा के मान ज्ञात कीजिए |

The correct Answer is: वर्ग इकाई
चित्र से स्पष्ट है कि
के सापेक्ष अवकलन करने पर
बिंदु जहाँ तथा प्रतिच्छेद करते है, होंगे
या
हम कह सकते है कि
वर्ग इकाई
वर्ग इकाई
वर्ग इकाई
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - AREA UNDER THE CURVEEXERCISE - Do yourself-14videos
AREA UNDER THE CURVE
- BOOK - ALLEN HINDICHAPTER - AREA UNDER THE CURVEEXERCISE - Do yourself-23videos
AREA UNDER THE CURVE
- BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - EXERCISE -05 [B] (JEE ADVANCED : PREVIOUS YEAR QUESTIONS)29videos
3D-COORDINATE GEOMETRY
- BOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE 5 (B) JEE (ADVANCED) : PREVIOUS YEAR QUESTIONS36videos
COMPLEX NUMBER
Similar Questions
वक्र y=x2+2 द्वारा x-अक्ष के ऊपर कोटियो x=2 व् x=3 के मध्य परिबद्ध क्षेत्रफल ज्ञात कीजिए |
04:22View Solutionवक्रो y=√x तथा y=x द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिए |
03:29View Solution(a) उस समतल का समीकरण ज्ञात कीजिए जो बिन्दुओं (2,1,0),(5,0,1) और (4,1,1) से गुजरता हो। (b) यदि बिन्दु P(2, 1, 6) है, तो बिन्दु Q ज्ञात कीजिए ताकि PQ, समतल (a) के लम्बवत् हो तथा PQ का मध्य बिन्दु उस पर स्थित हो।
10:51View Solutionयदि z1,z2,z3 सम्मिश्र संख्याएँ इस प्रकार है कि |z1|=|z2|=|z3|=∣∣∣1z1+1z2+1z3∣∣∣=1, तब |z1+z2+z3| है:
05:14View Solutionवह स्थानांतरण ज्ञात कीजिए कि मूलबिंदु को एक उचित बिंदु पर हटाकर दो रेखाओ के समीकरण x+y=1 तथा x−y=1 को x+y=0 तथा x−y=0 के रूप में लिखा जा सके ।
03:13View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
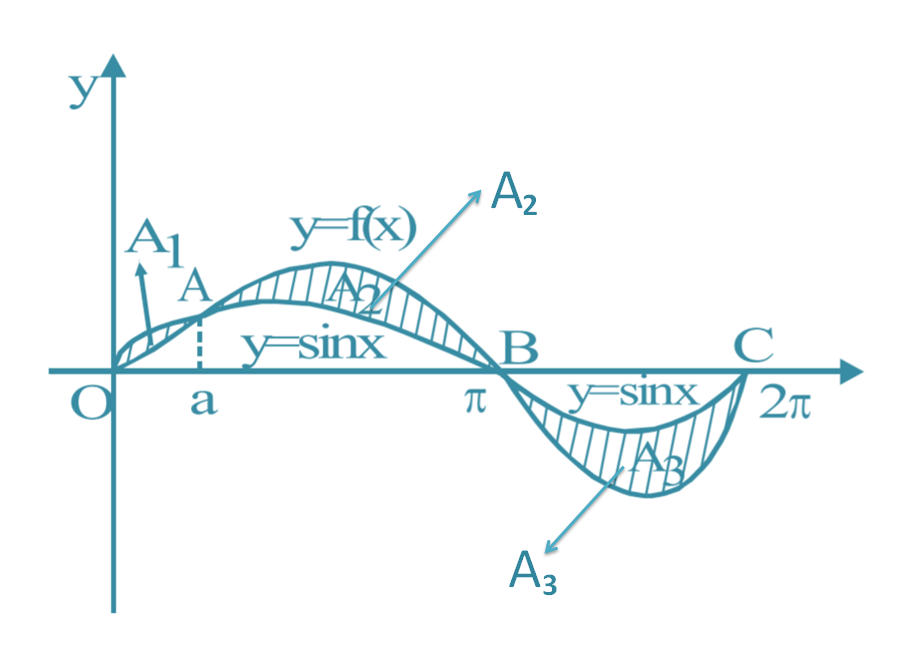
01:52View SolutionIn the adjacent figure the graph of two function y=f(x) and y=sinx are given y=sin x intersects, y=f(x) at A(a,f(a)),B(π,0)andC(2π,0).
Ai(i=1,2,3) is the area bounded by the curves y=f(x)andy=sinx between x=0 and x=a,i=1 between x=a and x=π,i=2 between x=π and x=2π,i=3. If A1=1−sina+(a−1) cos a, determine the function f(x). Hence, determine a and A1. Also, calculate A2andA3.
 .02:00View Solution
.02:00View Solutionयदि f तथा g दो फलन निम्न प्रकार से परिभाषित हैं :
f(x)=xx−1 तथा g(x)=1x−3 जहाँ x∈R तो gof तथा fog ज्ञात कीजिए तथा उनके डोमेन भी लिखिए ।01:58View Solutionयदि फलन f तथा g निम्न प्रकार परिभाषित हो, तो fog तथा gof ज्ञात कीजिए:
f(x)=logx,g(x)=ex04:40View Solutionयदि फलन f तथा g निम्न प्रकार परिभाषित हो, तो fog तथा gof ज्ञात कीजिए:
f(x)=x3,g(x)=sinx03:56View Solutionयदि फलन f तथा g निम्न प्रकार परिभाषित हो, तो fog तथा gof ज्ञात कीजिए:
f(x)=cosx,g(x)=|sinx|03:04View Solutionयदि फलन f तथा g निम्न प्रकार परिभाषित हो, तो fog तथा gof ज्ञात कीजिए:
f(x)=ex,g(x)=x+205:10View Solutionवक्र y=2√x तथा x=0,x=1 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
05:17View Solutionवक्र y=√4−x2,x=√3y तथा x-अक्ष के मध्य घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
02:39View Solutionx तथा y के मान ज्ञात कीजिए यदि -
sin−1x+sin−1y=π2
cos−1x−cos−1y=002:46View Solutionx के किन मानों के लिए फलन f(x)=x1+x2 वर्धमान तथा ह्रासमान है।
02:38View Solution
