Light of wavelength λ from a point source falls on a small circular rings around a central bright spot are formed on a screen beyond the obstacle The distance between the screen and obstacle is D. Then, the condition for the formation of rings, is
√λ≈d4D
λ≈d24D
d≈λ2D
λ≈D4
The correct Answer is:B
To solve the problem of determining the condition for the formation of circular rings around a central bright spot when light of wavelength λ falls on a small circular obstacle, we can follow these steps:
1. Understand the Setup:
- We have a point source of light emitting waves of wavelength λ.
- There is a small circular obstacle that causes diffraction, leading to the formation of a central bright spot and surrounding rings on a screen located at a distance D from the obstacle.
2. Identify the Condition for Ring Formation:
- The formation of rings (or fringes) is a result of constructive and destructive interference of the light waves that pass around the obstacle.
- The condition for constructive interference (bright rings) can be derived from the geometry of the setup.
3. Apply the Formula for Ring Formation:
- The radius of the nth ring can be expressed in terms of the wavelength and the distance D using the formula:
r2n=nλD
- Here, rn is the radius of the nth ring, and n is an integer representing the ring number.
4. Relate the Radius to the Wavelength:
- For the first ring (where n=1):
r21=λD
- For higher order rings, the relationship remains similar, with n increasing.
5. Express the Wavelength in Terms of the Distance:
- Rearranging the formula gives:
λ=r2nD
- This indicates that the wavelength λ is dependent on the square of the radius of the ring and the distance D.
6. Final Condition for Formation of Rings:
- To find the specific condition for the formation of rings, we can express it as:
λ=D24D
- This simplifies to:
λ=D4
- Thus, the condition for the formation of rings is that the wavelength λ should be approximately equal to D24D.
Conclusion:
The condition for the formation of circular rings around a central bright spot is given by:
λ=D24D
- We have a point source of light emitting waves of wavelength λ.
- There is a small circular obstacle that causes diffraction, leading to the formation of a central bright spot and surrounding rings on a screen located at a distance D from the obstacle.
- The formation of rings (or fringes) is a result of constructive and destructive interference of the light waves that pass around the obstacle.
- The condition for constructive interference (bright rings) can be derived from the geometry of the setup.
- The radius of the nth ring can be expressed in terms of the wavelength and the distance D using the formula:
r2n=nλD
- Here, rn is the radius of the nth ring, and n is an integer representing the ring number.
- For the first ring (where n=1):
r21=λD
- For higher order rings, the relationship remains similar, with n increasing.
- Rearranging the formula gives:
λ=r2nD
- This indicates that the wavelength λ is dependent on the square of the radius of the ring and the distance D.
- To find the specific condition for the formation of rings, we can express it as:
λ=D24D
- This simplifies to:
λ=D4
- Thus, the condition for the formation of rings is that the wavelength λ should be approximately equal to D24D.
The condition for the formation of circular rings around a central bright spot is given by:
λ=D24D
Topper's Solved these Questions
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE main (Only one option is Correct )
22 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced Only one option is correct
22 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - match column
4 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER
22 Videos
Similar Questions
A beam of light of wavelength 600 nm from a distant source falls on a single slit 1.0 mm wide and the resulting diffraction pattern is observed on a screen 2 m away What is the distance between the second bright fringe on either side of the central bright fringe ?
View SolutionA beam of light of wavelength 600 nm from a distance source falls on a single slit 1 mm wide and resulting diffraction pattern is observed on a screen 2m away. What is the distance between the first bright fringes on either side of the central bright fringe ?
View Solution
Knowledge Check
A beam of light of wavelength 600 nm from a distant source
falls on a single slit 1.0 mm wide and the resulting diffraction pattern is
observed on a screen 2m away. What is the distance between the first dark
fringe on either side of the central bright fringe?A1.2cmB1.2mmC2.4cmD2.4mm
A beam of light of wavelength 600 nm from a distant source falls on a single slit 1 mm wide and the resulting diffraction pattern is observed on a screen 2 m away. The distance between the first dark fringes on either side of the central bright fringe is
View SolutionA beam of light of wavelength 600 nm from a distant source
falls on a single slit 1.0 mm wide and the resulting diffraction pattern is
observed on a screen 2m away. What is the distance between the first dark
fringe on either side of the central bright fringe?
View SolutionA beam of light of wavelength 600 nm from a distance source falls on a single slit 2 mm wide and the resulting diffraction pattern is observed on a screen 2m away. What is the distance between the first dark fringes on either side of central bright fringe ?
View SolutionWhen a plane wave front of light, of wavelength λ, is incident on a narrow slit, an intensity distribution pattern, of the form shown is observed on a screen, suitably kept behind the slit. Name the phenomenon observed.
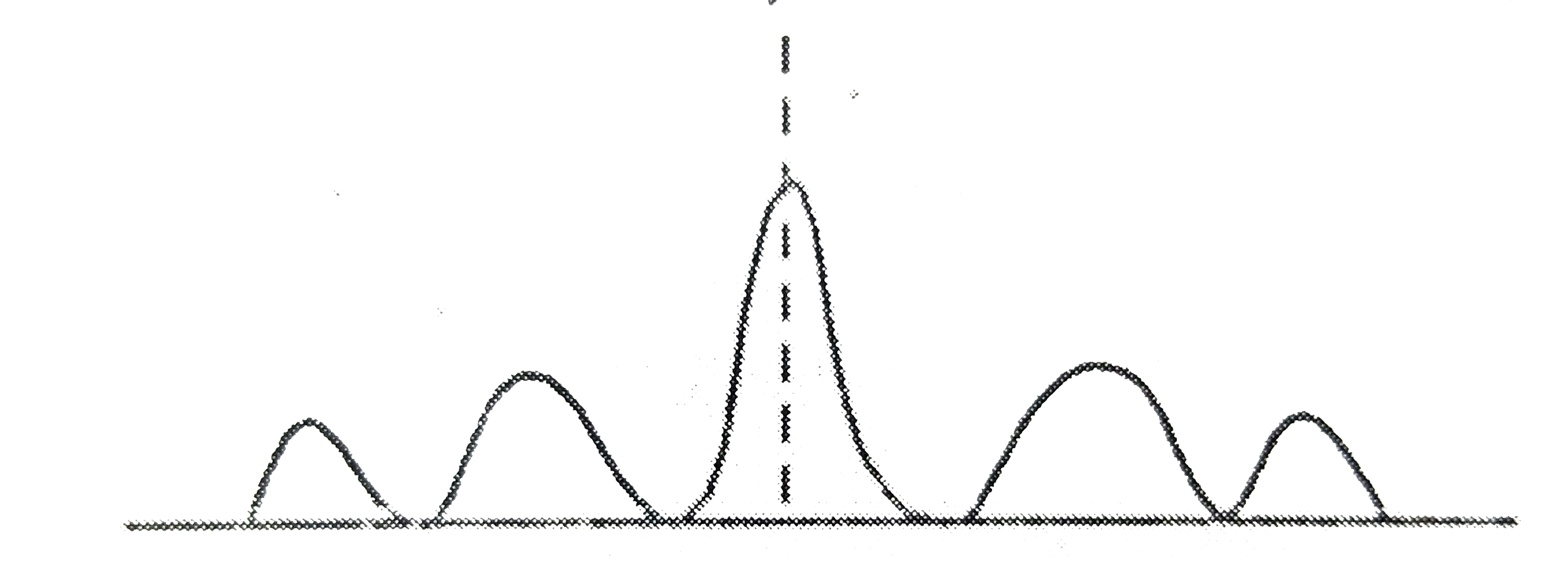
(a) Obtain the conditions for the formation of central maximum and secondary maxima and the minima.
(b) Why is there significant fall in intensity of the secondary maxima compared to the central maximum, whereas in double slit experiment all the bright fringes are of the same intensity ?
(c) When the width of the slit is made double the original width, how is the size of the central band affected ?
View SolutionA beam of light of wavelength 600nm from a distance source falls on a single slit 1mm wide and a resulting diffraction pattern is observed on a screen 2m away. The distance between the first dark frings on either side of central bright fringe is
View SolutionLight of wavelength λ is incident on a slit of width d and distance between screen and slit is D. Then width of maxima and width of slit will be equal if D is
View SolutionLight of wavelength 5000 Å is incident on a slit of width 0.1 mm. Find out the width of the central bright line on a screen distance 2m from the slit?
View Solution
