A radioactive substance emit 100 beta particfles in the first 2 s and 50 beta particles in the next 2s. The mean life of the sample is
4 s
2 s
20.693s
2×0.693s
The correct Answer is:C
To find the mean life of the radioactive substance based on the given information, we can follow these steps:
Step 1: Understand the decay process
The problem states that a radioactive substance emits 100 beta particles in the first 2 seconds and 50 beta particles in the next 2 seconds. This indicates that the substance is undergoing radioactive decay.
Step 2: Determine the half-life
From the information given:
- In the first 2 seconds, 100 particles are emitted.
- In the next 2 seconds, 50 particles are emitted.
This suggests that after the first 2 seconds, the number of particles remaining is:
N0−100=N
Where N0 is the initial number of particles.
After the next 2 seconds, the number of particles remaining is:
N−50=N′
Since 100 particles were emitted in the first 2 seconds, we can infer that the initial count of particles was 100. After 2 seconds, there are 0 particles left, indicating that the half-life is indeed 2 seconds.
Step 3: Relate half-life to decay constant
The relationship between half-life (t1/2) and the decay constant (λ) is given by:
t1/2=ln(2)λ
Step 4: Calculate the decay constant
From the half-life, we can rearrange the formula to find λ:
λ=ln(2)t1/2
Substituting t1/2=2 seconds:
λ=ln(2)2
Step 5: Calculate the mean life
The mean life (τ) is related to the decay constant by:
τ=1λ
Substituting for λ:
τ=1ln(2)2=2ln(2)
Step 6: Substitute the value of ln(2)
We know that ln(2)≈0.693:
τ=20.693
Step 7: Calculate the final result
Now, we can compute the mean life:
τ≈20.693≈2.885 seconds
Thus, the mean life of the sample is approximately 2.885 seconds.
Summary of the Solution Steps:
1. Understand the decay process and the emitted particles.
2. Determine the half-life based on the emitted particles.
3. Relate half-life to the decay constant.
4. Calculate the decay constant using the half-life.
5. Use the decay constant to find the mean life.
6. Substitute the value of ln(2) to find the mean life.
The problem states that a radioactive substance emits 100 beta particles in the first 2 seconds and 50 beta particles in the next 2 seconds. This indicates that the substance is undergoing radioactive decay.
From the information given:
- In the first 2 seconds, 100 particles are emitted.
- In the next 2 seconds, 50 particles are emitted.
N0−100=N
Where N0 is the initial number of particles.
N−50=N′
The relationship between half-life (t1/2) and the decay constant (λ) is given by:
t1/2=ln(2)λ
From the half-life, we can rearrange the formula to find λ:
λ=ln(2)t1/2
Substituting t1/2=2 seconds:
λ=ln(2)2
The mean life (τ) is related to the decay constant by:
τ=1λ
Substituting for λ:
τ=1ln(2)2=2ln(2)
We know that ln(2)≈0.693:
τ=20.693
Now, we can compute the mean life:
τ≈20.693≈2.885 seconds
1. Understand the decay process and the emitted particles.
2. Determine the half-life based on the emitted particles.
3. Relate half-life to the decay constant.
4. Calculate the decay constant using the half-life.
5. Use the decay constant to find the mean life.
6. Substitute the value of ln(2) to find the mean life.
Topper's Solved these Questions
Similar Questions
A radioactive substance emits n beat particles in the first 2 s and 0.5 n beta particles in the next 2 s. The mean life of the sample is
View SolutionRadioactive nuclei emit β−1 particles.
Electrons exist inside the nucleus.View SolutionRadioactive nuclei emit β−1 particles.
Electrons exist inside the nucleus.View Solution(a) Calculate the activity of one mg sample .28Sr90 whose half life period is 28 years.
(b) An experiment is performed to determine the half-life of a radioactive substance which emits one beta particle for each decay process. Observation shown that an average of 8.4β−particles are emitted each second by 2.5mg of the substance. the atomic weight of the substance is 230. calculate the half0life of the substance.
(c) Determine the quantity of .84Po210 necessary to provide a source of alpha particle of 5mCi strength (T1/2 for Po =138 day).View SolutionTwo identical nuclei A and B of the same radioactive element undergo β decay. A emits a β-particle and changes to A'. B emits a β-particle and then a γ-photon immediately afterwards, and changes to B'
View SolutionAssertion :Radioactive nuclei emit β−1 particles.
Reason :Electrons exist inside the nucleus.View SolutionFrom a radioactive substance x numbers of α-particles any y numbers of β-particles are emitted. As a result atomic number decreases by n and mass number by m. Then, match the following two columns.
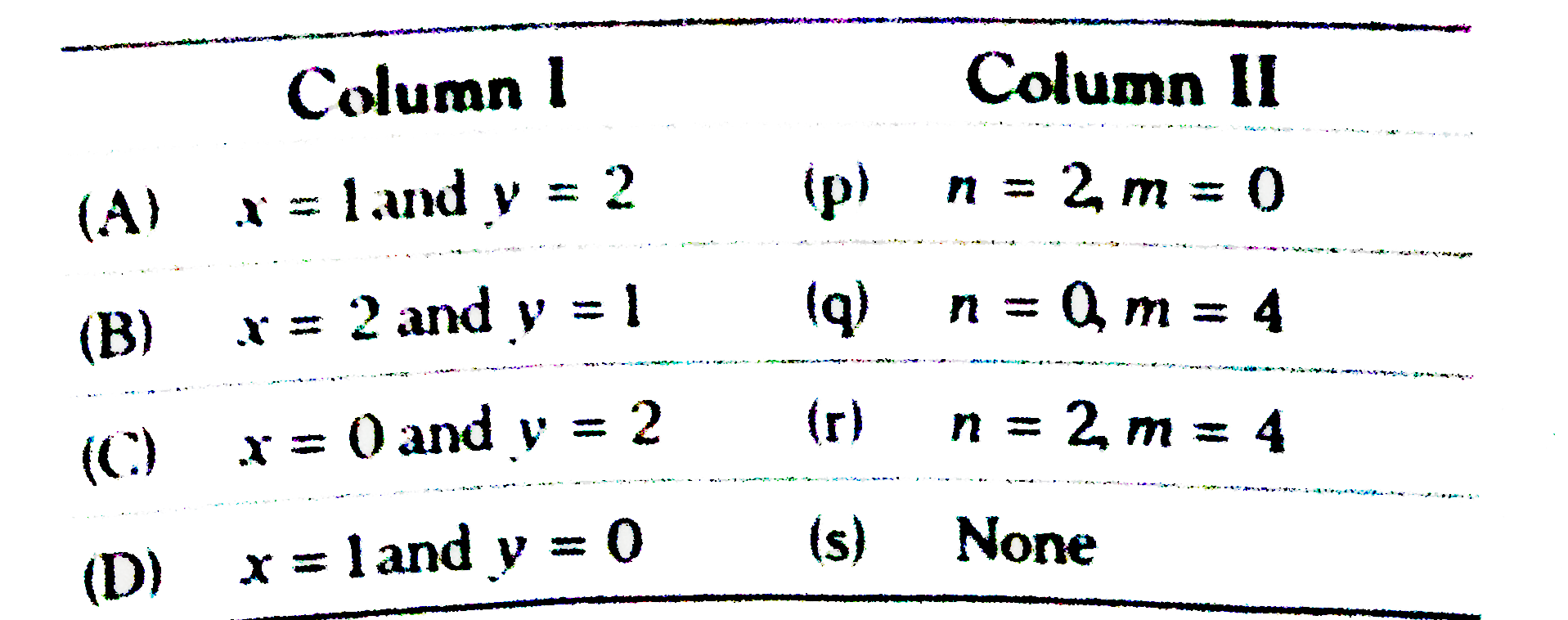 View Solution
View SolutionA radioactive element decays by β−emission. A detector records n beta particles in 2 s and in next 2 s it records 0.75 n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionA radioactive element .90X238 decay into .83Y222. The number of β−particles emitted are.
View Solution78th of the active nuclei present in a radioactive sample has decayed in 8 s. The half-life of the sample is
View Solution
