According to Moseley's law, the ratio of the slope of graph between √f and Z for Kβ and Kα is
√3227
√2732
√536
√365
The correct Answer is:A
To solve the problem of finding the ratio of the slope of the graph between √f and Z for Kβ and Kα according to Moseley's law, we can follow these steps:
1. Understand Moseley's Law:
Moseley's law states that the square root of the frequency (√f) of the emitted X-ray is proportional to the atomic number (Z) of the element. The general formula is given by:
√f=√R⋅(Z−1)⋅
⎷(1n21−1n22)
where R is a constant, and n1 and n2 are principal quantum numbers.
2. Identify Quantum Numbers for Kβ and Kα:
- For Kβ: n1=1, n2=3
- For Kα: n1=1, n2=2
3. Write the Equation for Kβ:
√fβ=√R⋅(Z−1)⋅√(112−132)
Calculate the term:
112−132=1−19=89
Thus,
√fβ=√R⋅(Z−1)⋅√89=√R⋅(Z−1)⋅2√23
4. Write the Equation for Kα:
√fα=√R⋅(Z−1)⋅√(112−122)
Calculate the term:
112−122=1−14=34
Thus,
√fα=√R⋅(Z−1)⋅√34=√R⋅(Z−1)⋅√32
5. Find the Ratio √fβ√fα:
√fβ√fα=√R⋅(Z−1)⋅2√23√R⋅(Z−1)⋅√32
The common terms √R and (Z−1) cancel out:
=2√23⋅2√3=4√23√3
6. Simplify the Ratio:
=4√23√3=4√69
Final Answer:
The ratio of the slope of the graph between √f and Z for Kβ and Kα is:
4√69
Moseley's law states that the square root of the frequency (√f) of the emitted X-ray is proportional to the atomic number (Z) of the element. The general formula is given by:
√f=√R⋅(Z−1)⋅
⎷(1n21−1n22)
where R is a constant, and n1 and n2 are principal quantum numbers.
- For Kβ: n1=1, n2=3
- For Kα: n1=1, n2=2
√fβ=√R⋅(Z−1)⋅√(112−132)
Calculate the term:
112−132=1−19=89
Thus,
√fβ=√R⋅(Z−1)⋅√89=√R⋅(Z−1)⋅2√23
√fα=√R⋅(Z−1)⋅√(112−122)
Calculate the term:
112−122=1−14=34
Thus,
√fα=√R⋅(Z−1)⋅√34=√R⋅(Z−1)⋅√32
√fβ√fα=√R⋅(Z−1)⋅2√23√R⋅(Z−1)⋅√32
The common terms √R and (Z−1) cancel out:
=2√23⋅2√3=4√23√3
=4√23√3=4√69
The ratio of the slope of the graph between √f and Z for Kβ and Kα is:
4√69
Topper's Solved these Questions
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - ASSERTION AND REASON
10 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MATCH THE COLUMNS
4 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - Check point 12.3
15 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN
62 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
Similar Questions
According to Moseley.s law, the frequency of a spectral line in X-ray spectrum varies as
View SolutionAccording to moselay.s law, the frequency (ϑ) of the Kα line and the atomic number (z) of the element have the relation (A and B) are constants
View SolutionIn Moseley's law √v=a(z−b), the volue of the screening constant for K-series and L-series of X-rays are respectively
View Solution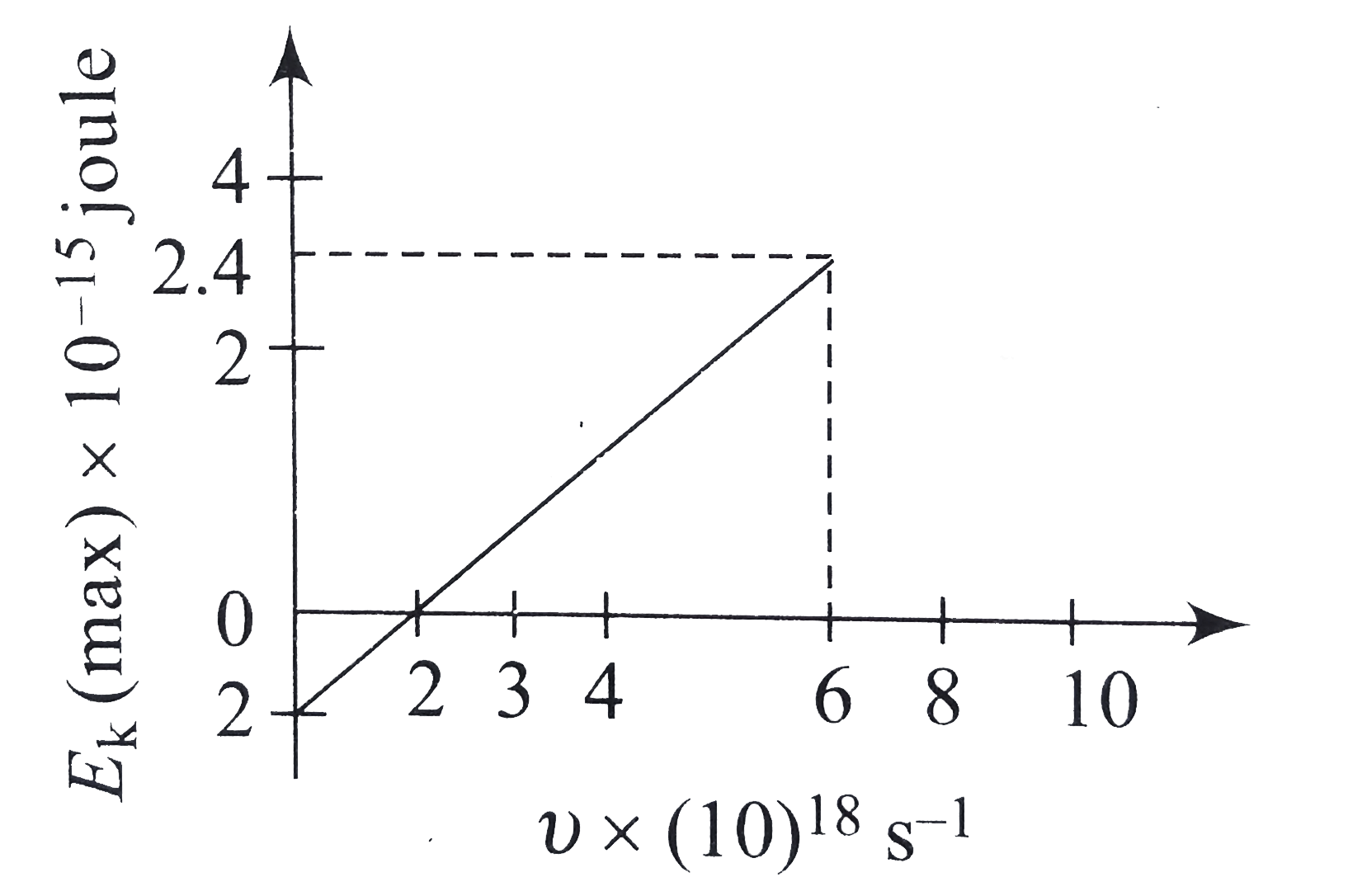
In the experiment on photoelectric effect, the graph between EK(max) and v is found to be a straight line as sshoen in fig. The threshold frequency and Planck's constant according to this graph are
View SolutionIn the Moseley relation, √v=a(Z−b) which will have the greater value for the constant a for Kα or Kβ transition?
View SolutionMoseley's law for characteristic X-rays is √v=a(Z−b). In this,
View SolutionUse Moseley's law with b=1 to find the frequency of the Kα X-rays of La (Z=57) , if the frequency of the Kα X-rays of Cu (Z=29) is know to be 1.88×1018Hz.
View SolutionUse Moseley's law with b = 1 to find the frequency of the Kα X-ray of La(Z=57) if the frequency of the Kα X-ray of Cu(Z=29) is known to be 1⋅88×1018 Hz.
View SolutionUse Moseley's law with b = 1 to find the frequency of the Kα X-ray of La(Z=57) if the frequency of the Kα X-ray of Cu(Z=29) is known to be 1⋅88×1018 Hz.
View SolutionFigure shown Moseley's plot between √f and Z where f is the frequency and Z is the atomic number. Three lines A, B, and C always in the graph may repersent

View Solution
