Assertion : The refractive index of diamond is √6 and that of liquid is √3 . If the light travels from diamond to the liquid, it will totally reflected when the angle of incidence is 30∘.
Reason : μ=1sinC, where μ is the refractive index of diamond with respect to liquid.
If both Assertion and Reason are true and Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:D
To solve the problem, we need to analyze both the assertion and the reason provided in the question.
Step 1: Understanding the Assertion
The assertion states that the refractive index of diamond is √6 and that of the liquid is √3. We need to determine if total internal reflection (TIR) occurs when light travels from diamond to the liquid at an angle of incidence of 30∘.
Step 2: Calculate the Critical Angle
To find the critical angle θc for total internal reflection, we use the formula:
sinθc=n2n1
where n1 is the refractive index of diamond and n2 is the refractive index of the liquid.
Substituting the values:
n1=√6,n2=√3
sinθc=√3√6=√3√2⋅3=1√2=√22
Thus, the critical angle θc can be calculated as:
θc=sin−1(√22)=45∘
Step 3: Compare the Angle of Incidence with the Critical Angle
The angle of incidence given is 30∘. Since 30∘<45∘, the angle of incidence is less than the critical angle.
Step 4: Conclusion on the Assertion
Since the angle of incidence is less than the critical angle, total internal reflection will not occur. Therefore, the assertion is false.
Step 5: Analyzing the Reason
The reason states that μ=1sinC, where μ is the refractive index of diamond with respect to the liquid. This is a correct statement, as it relates the refractive indices and the critical angle.
Final Conclusion
- The assertion is false.
- The reason is true.
Thus, the correct answer is that the assertion is false, and the reason is true.
---
The assertion states that the refractive index of diamond is √6 and that of the liquid is √3. We need to determine if total internal reflection (TIR) occurs when light travels from diamond to the liquid at an angle of incidence of 30∘.
To find the critical angle θc for total internal reflection, we use the formula:
sinθc=n2n1
where n1 is the refractive index of diamond and n2 is the refractive index of the liquid.
n1=√6,n2=√3
sinθc=√3√6=√3√2⋅3=1√2=√22
Thus, the critical angle θc can be calculated as:
θc=sin−1(√22)=45∘
The angle of incidence given is 30∘. Since 30∘<45∘, the angle of incidence is less than the critical angle.
Since the angle of incidence is less than the critical angle, total internal reflection will not occur. Therefore, the assertion is false.
The reason states that μ=1sinC, where μ is the refractive index of diamond with respect to the liquid. This is a correct statement, as it relates the refractive indices and the critical angle.
- The assertion is false.
- The reason is true.
Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Medical entrance gallary
Explore 76 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Exercise
Explore 170 Videos
- NUCLEIBook:DC PANDEY ENGLISHChapter:NUCLEIExercise:C MADICAL ENTRANCES GALLERY
Explore 46 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
Similar Questions
Knowledge Check
The refractive index of a medium is √3. What is the angle of refraction, if unpolarizing light is incident on the polarising angle of the medium ?
A60∘B45∘C30∘D0∘
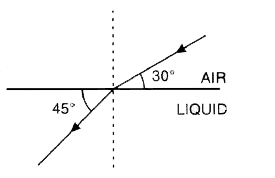
The diagram alongside shows the refraction of a ray of light from air to a liquid.
(a) Write the values of (i) angle of incidence, and (ii) angle of refraction.
(b) Use snell's law to find the refractive index of liquid with respect to air.
View SolutionA light ray is travelling from air to glass. True reflected and refracted rays are perpendicular to each other. If the angle of incidence in air is I the refractive index of glass is
View SolutionA ray of light falls on a transparent glass slab of refractive index √2. If the reflected and refracted rays are mutually perpendicular, then the angle of incidence is
View SolutionThe refractive index of air with respect to glass is 2/3. The refractive index of diamond with respect to air is 12/5. Then the refractive index of glass with respect to diamond will be
View SolutionA lens of refractive index μ is put in a liquid of refractive index μ'. If focal length of lens in air is f, its focal length in liquid will be.
View SolutionThe refractive index of diamond is 2.42, whereas for air it is 1.0. What does it tell you about optical density and speed of light in air and in diamond?
View SolutionA liquid is placed in a hollow prism of angle 60∘. If angle of the minimum deviation is 30 what is the refractive index of the liquid?
View Solution

