Question

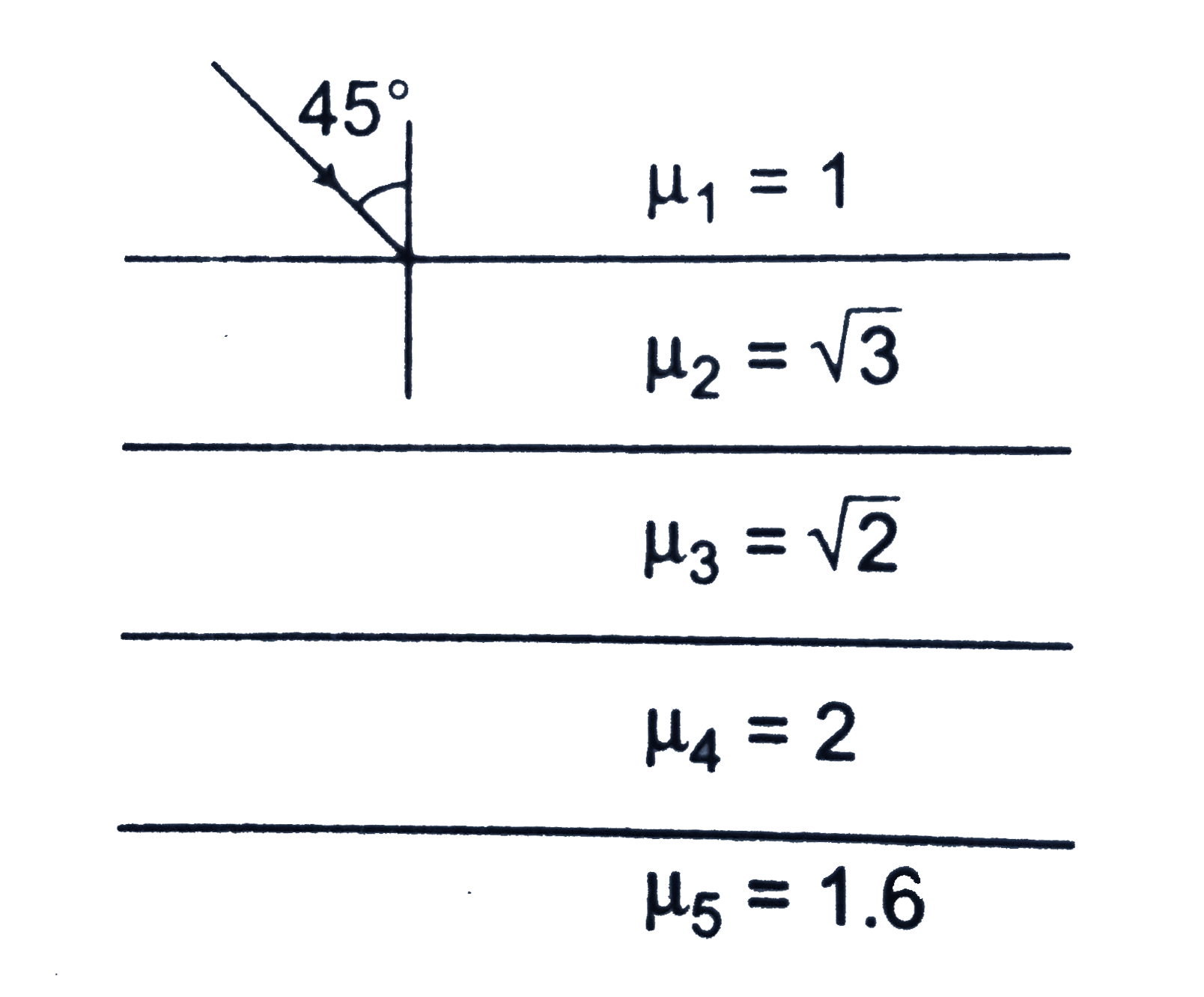
${}_i{u}_j$ represents refractive index when a light ray goes from medium I to medium j, then the product ${}_2{\mu }_1\times$${}_3{\mu }_2\times$${}_4{\mu }_3$ is equal to

Options

A. `""_(3)µ_(1)`
B. `""_(3)µ_(2)`
C. `(1)/(""_(1)µ_(4))`
D. `""_(4)µ_(2)`

Answer

C

Explanation

To solve the problem, we need to analyze the refractive indices given in the question. The refractive index $${\mu }_{ij}$$ is defined as the ratio of the refractive index of medium $$j$$ to that of medium $$i$$.

Let's break down the problem step by step:

Step 1: Understand the definition of refractive index
The refractive index \( \mu_{ij} \) is defined as:
\( \mu_{ij} = \frac{n_j}{n_i} \)
where \( n_j \) is the refractive index of medium \( j \) and \( n_i \) is the refractive index of medium \( i \).

Step 2: Write down the refractive indices for the given products
We need to find the product \( \mu_{21} \mu_{32} \mu_{43} \):
- \( \mu_{21} = \frac{n_2}{n_1} \)
- \( \mu_{32} = \frac{n_3}{n_2} \)
- \( \mu_{43} = \frac{n_4}{n_3} \)

Step 3: Substitute the definitions into the product
Now, substituting these definitions into the product:
\( \mu_{21} \mu_{32} \mu_{43} = \left(\frac{n_2}{n_1}\right) \left(\frac{n_3}{n_2}\right) \left(\frac{n_4}{n_3}\right) \)

Step 4: Simplify the expression
When we multiply these fractions, we notice that \( n_2 \) in the numerator of \( \mu_{21} \) and the denominator of \( \mu_{32} \) cancels out, and \( n_3 \) in the numerator of \( \mu_{32} \) and the denominator of \( \mu_{43} \) also cancels out:
\( \mu_{21} \mu_{32} \mu_{43} = \frac{n_4}{n_1} \)

Step 5: Relate the result to the refractive index
The expression \( \frac{n_4}{n_1} \) can be rewritten in terms of the refractive index \( \mu_{14} \):
\( \frac{n_4}{n_1} = \mu_{14} \)

Conclusion
Thus, we conclude that:
\( \mu_{21} \mu_{32} \mu_{43} = \mu_{14} \)

Final Answer
The product \( \mu_{21} \mu_{32} \mu_{43} \) is equal to \( \mu_{14} \).