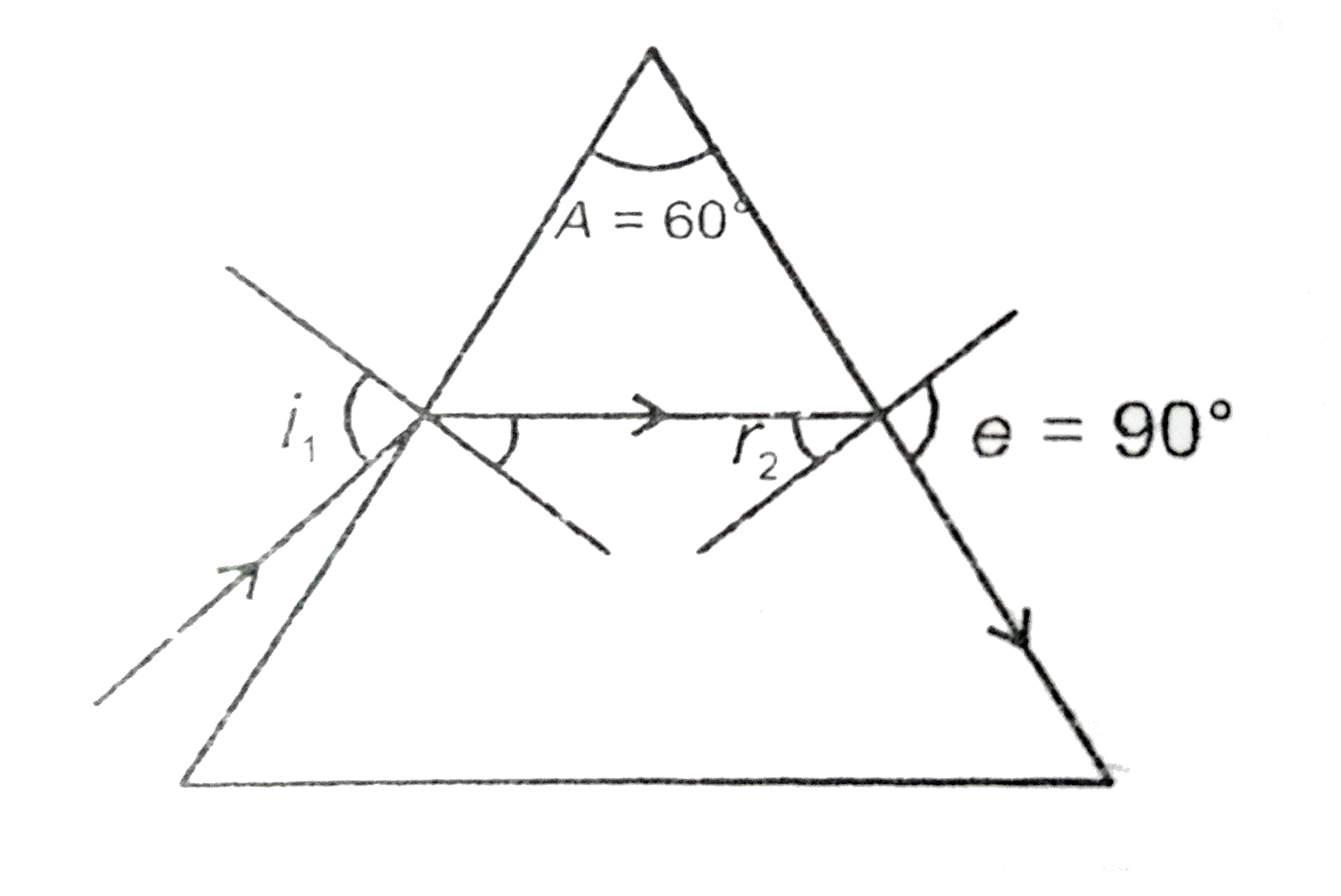
At what angle should a ray of light be incident on the face of a prism of refracting angle so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
To solve the problem of finding the angle of incidence I for a ray of light incident on a prism with a refracting angle of 60∘ and a refractive index of 1.524 such that it just suffers total internal reflection at the other face, we can follow these steps:
Step 1: Understand the Geometry of the Prism
The prism has a refracting angle A=60∘. When light enters the prism, it refracts at the first face (let's call it face AB) and then reaches the second face (face AC) where it will experience total internal reflection.
Step 2: Determine the Condition for Total Internal Reflection
For total internal reflection to occur at face AC, the angle of refraction r2 at this face must be 90∘. This means that the angle of incidence I1 at face AB and the angle of refraction r1 at face AC must satisfy the prism angle relationship:
A=I1+r1
Since r2=90∘, we have r1=90∘−r2=90∘−90∘=0∘.
Step 3: Use Snell's Law at Face AC
Using Snell's law at face AC:
n=sinI1sinr1
Where n is the refractive index of the prism (1.524), and r1 is the angle of refraction at face AC. Since r1=90∘:
n=sinI1sin90∘=sinI1
Thus,
sinI1=n
Substituting the value of n:
sinI1=1.524
This is not possible since the sine of an angle cannot exceed 1. Therefore, we need to find the angle of incidence I1 at face AB that leads to r1 being 90∘.
Step 4: Relate I1 and r1
Using the prism angle relation:
60∘=I1+r1
We can express r1 in terms of I1:
r1=60∘−I1
Step 5: Apply Snell's Law at Face AB
Using Snell's law at face AB:
nair⋅sinI=nprism⋅sinr1
Where nair=1 (the refractive index of air), we have:
sinI=n⋅sinr1
Substituting r1=60∘−I1:
sinI=1.524⋅sin(60∘−I1)
Step 6: Calculate I1
Now we can solve for I1 using the known values:
1. Calculate r1=60∘−I1.
2. Substitute into the equation and solve for I1.
Step 7: Solve the Equation
Using numerical methods or a calculator, we can find:
I1≈30∘
Final Answer
The angle at which the ray of light should be incident on the face of the prism is approximately 30∘.
---
The prism has a refracting angle A=60∘. When light enters the prism, it refracts at the first face (let's call it face AB) and then reaches the second face (face AC) where it will experience total internal reflection.
For total internal reflection to occur at face AC, the angle of refraction r2 at this face must be 90∘. This means that the angle of incidence I1 at face AB and the angle of refraction r1 at face AC must satisfy the prism angle relationship:
A=I1+r1
Since r2=90∘, we have r1=90∘−r2=90∘−90∘=0∘.
Using Snell's law at face AC:
n=sinI1sinr1
Where n is the refractive index of the prism (1.524), and r1 is the angle of refraction at face AC. Since r1=90∘:
n=sinI1sin90∘=sinI1
Thus,
sinI1=n
Substituting the value of n:
sinI1=1.524
This is not possible since the sine of an angle cannot exceed 1. Therefore, we need to find the angle of incidence I1 at face AB that leads to r1 being 90∘.
Using the prism angle relation:
60∘=I1+r1
We can express r1 in terms of I1:
r1=60∘−I1
Using Snell's law at face AB:
nair⋅sinI=nprism⋅sinr1
Where nair=1 (the refractive index of air), we have:
sinI=n⋅sinr1
Substituting r1=60∘−I1:
sinI=1.524⋅sin(60∘−I1)
Now we can solve for I1 using the known values:
1. Calculate r1=60∘−I1.
2. Substitute into the equation and solve for I1.
Using numerical methods or a calculator, we can find:
I1≈30∘
The angle at which the ray of light should be incident on the face of the prism is approximately 30∘.
Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Checkpoint 9.1
Explore 10 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Checkpoint 9.2
Explore 10 Videos
- NUCLEIBook:DC PANDEY ENGLISHChapter:NUCLEIExercise:C MADICAL ENTRANCES GALLERY
Explore 46 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
Similar Questions
A ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionCalculate the angle of incidence on the face of a prism of refracting angle 60∘ and of refractive index 1.5, for which the emergent ray just grazes the other face.
View Solution
Knowledge Check
A ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
A1.732B1.414C1.5D1.33
A ray of light is incident at 65∘ on one face of a prism of angle of 30∘ and the emergent ray makes 35∘ with the incident ray. The refractive index of the prism is:
View SolutionA ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
View SolutionA ray of light incident at an angle of incidence 48∘ on a prism of refracting angle 60∘ suffers minimum deviation. Calculate the angle of minimum deviation.
View SolutionA ray of monochromatic light is incident on the refracting face of a prism (angle 75∘0 . It passes through the prism and is incident on the other face at the critical angle. If the refractive index of the prism is √2 , then the angle of incidence on the first of the prism is
View Solution
A ray of light incident on one of the face of a prism as shown. After refraction through this surface ray is incident on base of the prism. The refractive index of the prism is √3. The net deviation of the ray due to prism is
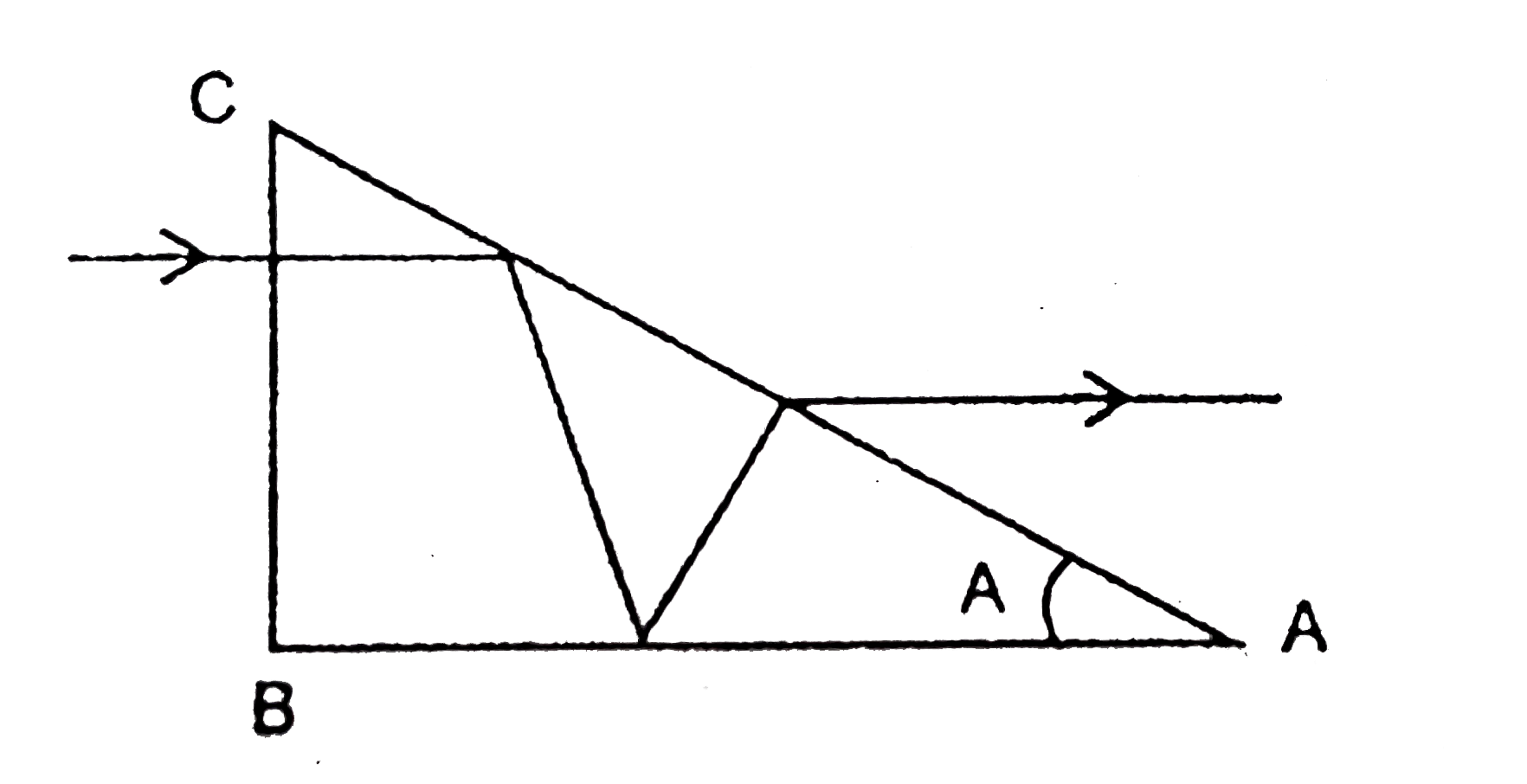
View SolutionA ray of light falls normally on one face of a right angled prims of refracting angle A. It suffers two total internal reflections before coming out of prism parallel to incident ray as shown. Refractive index to prism material will be:
View SolutionOne face of a prism with a refrective angle of 30∘ is coated with silver. A ray of light incident on another face at an angle of 45∘ is refracted and reflected from the silver coated face and retraces its path. What is the refractive index of the prism?
View Solution