A ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges and calculate the refractive index of the material of prism.
To solve the problem step by step, we will follow the principles of ray optics, particularly focusing on the behavior of light as it passes through a prism.
Step 1: Identify the Given Data
- Angle of incidence on the prism, I1=60∘
- Refracting angle of the prism, A=30∘
- Angle between the incident ray and the emergent ray, Δ=30∘
Step 2: Use the Relation Between Angles
The relationship between the angles in a prism can be expressed as:
Δ=I1+I2−A
Where:
- I2 is the angle of refraction inside the prism.
Substituting the known values:
30∘=60∘+I2−30∘
Step 3: Solve for I2
Rearranging the equation gives:
I2=30∘−60∘+30∘
I2=0∘
Step 4: Conclusion About the Emergent Ray
Since I2=0∘, this means that the ray emerges perpendicular to the face of the prism. Therefore, the emergent ray is indeed perpendicular to the face through which it emerges.
Step 5: Calculate the Refractive Index
Using Snell's law at the first surface of the prism:
μ=sinI1sinR1
Where:
- R1 is the angle of refraction at the first surface, which is equal to the angle of the prism A since I2=0∘.
Thus:
R1=A=30∘
Now substituting the values:
μ=sin60∘sin30∘
Step 6: Substitute the Values of Sine
Using known values:
- sin60∘=√32
- sin30∘=12
Substituting these into the equation gives:
μ=√3212=√3
Final Result
The refractive index of the material of the prism is μ=√3.
---
- Angle of incidence on the prism, I1=60∘
- Refracting angle of the prism, A=30∘
- Angle between the incident ray and the emergent ray, Δ=30∘
The relationship between the angles in a prism can be expressed as:
Δ=I1+I2−A
Where:
- I2 is the angle of refraction inside the prism.
30∘=60∘+I2−30∘
Rearranging the equation gives:
I2=30∘−60∘+30∘
I2=0∘
Since I2=0∘, this means that the ray emerges perpendicular to the face of the prism. Therefore, the emergent ray is indeed perpendicular to the face through which it emerges.
Using Snell's law at the first surface of the prism:
μ=sinI1sinR1
Where:
- R1 is the angle of refraction at the first surface, which is equal to the angle of the prism A since I2=0∘.
R1=A=30∘
μ=sin60∘sin30∘
Using known values:
- sin60∘=√32
- sin30∘=12
μ=√3212=√3
The refractive index of the material of the prism is μ=√3.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.1
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.2
10 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
A ray of light is incident at an angle of 60∘ on one face of a prism of angle 30∘. The ray emerging out of the prism makes an angle of 30∘ with the incident ray. The emergent ray is
View SolutionA ray of light is incident at an angle of 60∘ on one face of a prism which has refracting angle of 30∘ . The ray emerging out of the prism makes an angle of 30∘ with the incident ray. If the refractive index of the material of the prism is μ=√a , find the value of a .
View Solution
Knowledge Check
A ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
A1.732B1.414C1.5D1.33
A Ray of light is incident at an angle 60° on one face of a prism which has protecting angle of 30°. The emerging ray deviates through 30° from incident light. The refractive index of material of prism is
View SolutionA ray of light is incident on one face of a prism (m=√3) at an angle of 60∘. The refracting angle of the prism is also 60∘. Find the angle of emergence .
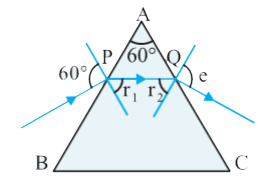
View SolutionA ray of light incident at an angle 90° with the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism
View SolutionA light ray is incident by grazing one of the face of a prism and after refraction ray does not emerge out, what should be the angle of prism while critical angle is C ?
View SolutionA ray of light is incident normally on one of the faces of a prism of apex angle 30 degree and refractive index √2. The angle of deviation of the ray in degrees is
View SolutionA ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
View SolutionA ray of light is incident at 65∘ on one face of a prism of angle of 30∘ and the emergent ray makes 35∘ with the incident ray. The refractive index of the prism is:
View Solution
