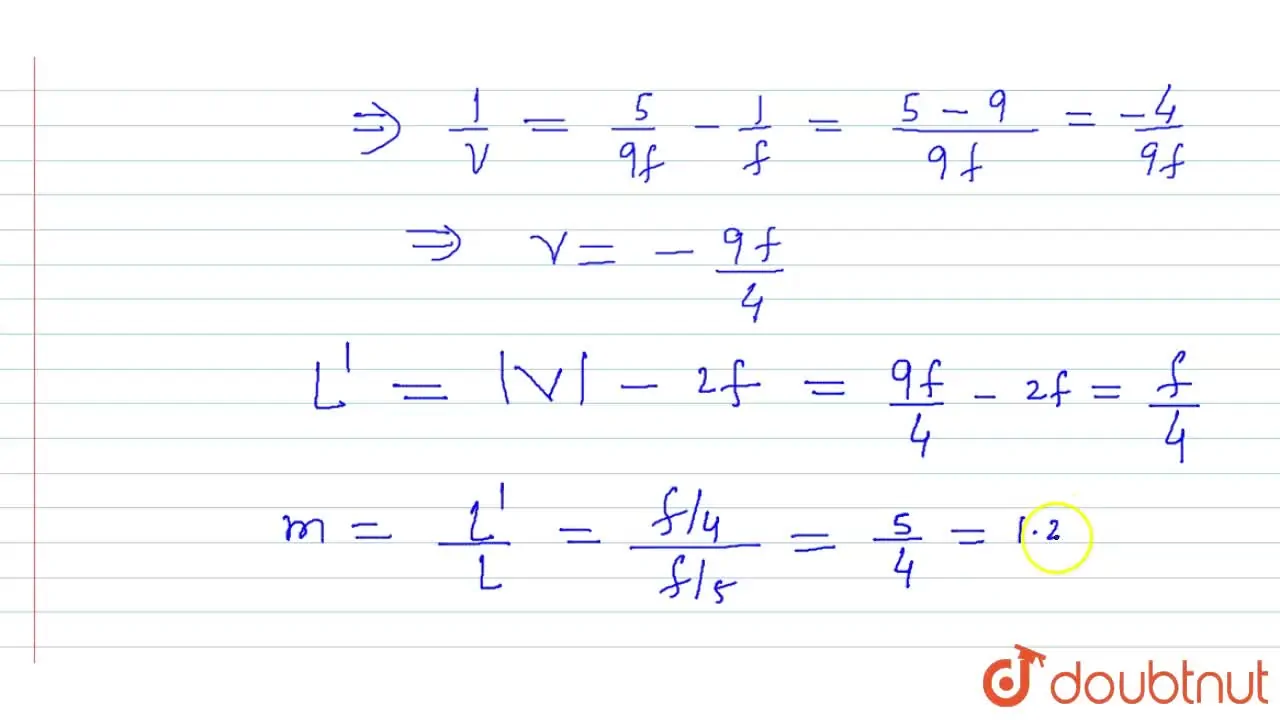A thin stick of length f/5 placed along the principal axis of a concave mirror of focal length f such that its image is real and elongated just touch the stick. What is the magnification?

One end of image concides with one end of stick i.e., either A or B is centre of curvature.
Since image is elongated i.e., point B is centre of curvature. Image of B is formed on B itself.
Image of A
u=−(2f−f/5)=−8f3,f=−f,v=?
1v+1u=1f⇒1v+1−8f/5=1−f
1v=−1f+58f=−8+58f=−38f⇒v=−8f3

Image length, A'B'=8f5−2f=−2f/5
Longitudinal magnification,
mL=−A'B'AB=2f/5f/5=2
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.110videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.210videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY46videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
Similar Questions
A thin rod of length f/3 is placed along the optical axis of a concave mirror of focal length f such that its image whichis real and elongated just touches the rod. Calculate the magnification.
View SolutionA thin rod of length d/3 is placed along the principal axis of a concave mirror of focal length = d such that its image, which is real and elongated, just touches the rod. Find the length of the image ?
View SolutionA thin rod of 5 cm length is kept along the axis of a concave mirror of 10 cm focal length such that its image is real and magnified and one end touches the rod. Its magnification will be
View SolutionA thin rod of 5 cm length is kept along the axis of a concave mirror of 10 cm focal length such that its image is real and magnified and one end touches to rod. Its magnification will be
View SolutionA thin rod of length (f3) is lying along the principal axis of a concave
mirror of focal length f.Image is real , magnified and inverted and one of the end or rod coincides with its image itself. Find length of the image.View SolutionThe image of an object placed on the principal axis of a concave mirror of focal length 12 cm is formed at a point which is 10cm more distance form the mirror than the object. The magnification of the image is
View SolutionAn object is placed on the principal axis of concave mirror of focal length 10 cm at a distance of 8.0 cm from the pole. Find the position and the nature of the image.
View SolutionA rod of length 10 cm lies along the principal axis of a concave mirror of focal length 10 cm in such a way that the end closer to the pole is 20 cm away from it. Find the length of the image.
View SolutionA rod of length 10 cm lies along the principal axis of a concave mirror of focal length 10 cm in such a way that its end closer to the pole is 20cm away from the mirror. The length of the image is
View SolutionA rod of length 10 cm lies along the principal axis of a concave mirror of focal length 10 cm in such a way that the end closer to the pole is 20 cm away from it. Find the length of the image.
View Solution