In an electrical circuit R,L,C and an AC voltage source are all connected in series. When L is removed from the circuit, the phase difference between the voltage and the current in the circuit is π/3. If instead, C is removed from the circuit, difference the phase difference is again π/3. The power factor of the circuit is
1/2
1/√2
1
√3/2
The correct Answer is:C
To solve the problem, we will analyze the circuit step by step, using the given information about the phase differences when either the inductor (L) or the capacitor (C) is removed.
Step 1: Analyze the first case (L is removed)
When the inductor (L) is removed, the circuit consists of the resistor (R) and the capacitor (C). The phase difference between the voltage and current is given as ϕ1=π3.
Using the relationship for the phase difference in an R-C circuit:
tanϕ1=XCR
where XC is the capacitive reactance.
Substituting ϕ1:
tan(π3)=XCR
We know that tan(π3)=√3, so:
√3=XCR
From this, we can express XC:
XC=√3R(Equation 1)
Step 2: Analyze the second case (C is removed)
When the capacitor (C) is removed, the circuit consists of the resistor (R) and the inductor (L). The phase difference is again given as ϕ2=π3.
Using the relationship for the phase difference in an R-L circuit:
tanϕ2=XLR
where XL is the inductive reactance.
Substituting ϕ2:
tan(π3)=XLR
Again, since tan(π3)=√3:
√3=XLR
From this, we can express XL:
XL=√3R(Equation 2)
Step 3: Relate the reactances
From Equations 1 and 2, we have:
XC=XL
This implies:
√3R=√3R
This indicates that the circuit is in resonance, where the inductive reactance equals the capacitive reactance.
Step 4: Calculate the power factor
In a resonant circuit, the impedance Z is equal to the resistance R:
Z=R
The power factor PF is given by:
PF=cosϕ=RZ
Since Z=R:
PF=RR=1
Conclusion
The power factor of the circuit is 1.
tanϕ1=XCR
where XC is the capacitive reactance.
tan(π3)=XCR
We know that tan(π3)=√3, so:
√3=XCR
From this, we can express XC:
XC=√3R(Equation 1)
tanϕ2=XLR
where XL is the inductive reactance.
tan(π3)=XLR
Again, since tan(π3)=√3:
√3=XLR
From this, we can express XL:
XL=√3R(Equation 2)
XC=XL
This implies:
√3R=√3R
This indicates that the circuit is in resonance, where the inductive reactance equals the capacitive reactance.
Z=R
The power factor PF is given by:
PF=cosϕ=RZ
Since Z=R:
PF=RR=1
Similar Questions
In an electrical circuit R,L, C and a.c voltage source are all connected in series. When L is removed from the circuit , the phase difference between the voltage and current in the circuit is π/6. If instead ,C is removed from the circuit , the phase difference is again π/6 . The power factor of the circuit is
View SolutionThe phase difference between voltage and current in series L-C circuit is
View Solution
Knowledge Check
Phase difference between voltage and current in a capacitor in an ac circuit is
AπBπ/2C0Dπ/3In a series LCR circuit, the phase difference between the voltage and the current is 45∘. Then the power factor will be
A0.607B0.707C0.808D1In series LCR circuit, the phase angle between supply voltage and current is
Atanϕ=XL−XCRBtanϕ=RXL−XCCtanϕ=RXL+XCDtanϕ=XL+XCR
Find the phase difference between voltage and current in L-C circuit.
View SolutionA seriesLCR circuit is connected to an ac voltage source. When L is removed from the circuit, the phase difference between current and voltage is π3. If instead C is removed from the circuit phase difference is again π3 between current and voltage. Power factor of circuit is:
View SolutionIn series LCR circuit, the phase difference between voltage across L and voltage across C is
View SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
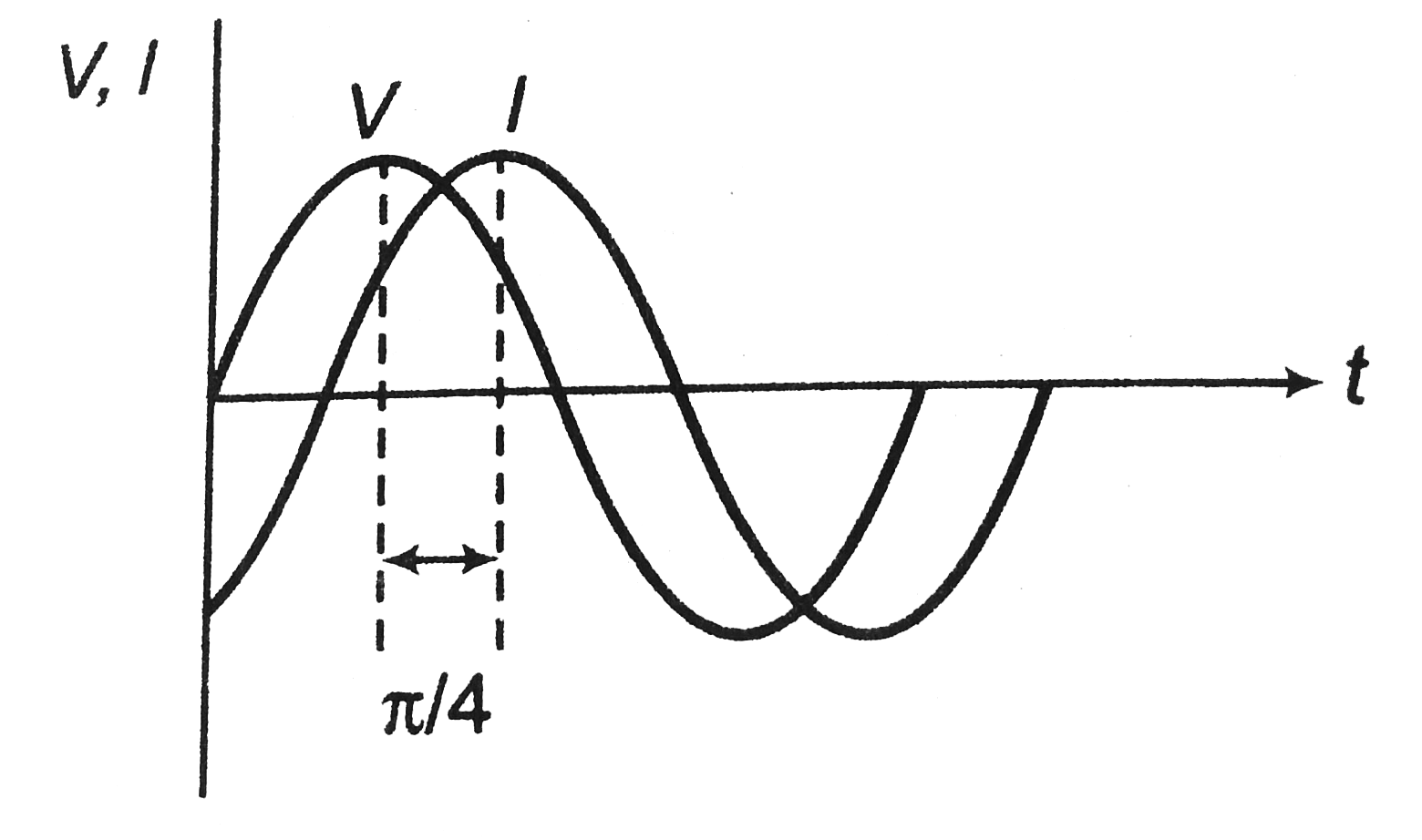 .
.
View SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
 .
.
View Solution