Current through an AC series L-C-R circuit is 2 A if operated at resonance frequency , and 1 A if operated at 50% less than resonant frequency . The current (in A) if the frequency is 100% more than the resonant frequency , is
A.√2 B.1 C.√3 D.Data insufficient
√2
1
√3
Data insufficient
The correct Answer is:B
To solve the problem, we need to analyze the behavior of the current in an AC series L-C-R circuit at different frequencies, specifically at resonance frequency and at frequencies that are 50% less and 100% more than the resonance frequency.
1. Identify the Resonance Condition:
At resonance frequency (ω₀), the inductive reactance (X_L) equals the capacitive reactance (X_C). This means:
XL=XC
2. Current at Resonance Frequency:
The current through the circuit at resonance frequency is given as:
I0=2A
3. Current at 50% Less than Resonance Frequency:
When the frequency is 50% less than the resonance frequency, the new frequency (ω') is:
ω′=ω02
At this frequency:
- The inductive reactance becomes:
X′L=XL2
- The capacitive reactance becomes:
X′C=2XC
4. Calculate the Total Impedance at 50% Less Frequency:
The total impedance (Z') at this frequency is given by:
Z′=R+j(X′C−X′L)=R+j(2XC−XL2)
Since we know that at resonance XC=XL, we can substitute XC with XL:
Z′=R+j(2XL−XL2)=R+j(4XL2−XL2)=R+j(3XL2)
5. Current at 50% Less Frequency:
The current at this frequency is given as:
I′=1A
Using Ohm's law:
I′=VZ′
6. Current at 100% More than Resonance Frequency:
When the frequency is 100% more than the resonance frequency, the new frequency (ω'') is:
ω′′=2ω0
At this frequency:
- The inductive reactance becomes:
X′′L=2XL
- The capacitive reactance becomes:
X′′C=XC2
7. Calculate the Total Impedance at 100% More Frequency:
The total impedance (Z'') at this frequency is:
Z′′=R+j(X′′C−X′′L)=R+j(XC2−2XL)
Again substituting XC with XL:
Z′′=R+j(XL2−2XL)=R+j(XL−4XL2)=R+j(−3XL2)
8. Determine the Current at 100% More Frequency:
The current at this frequency can be expressed as:
I′′=VZ′′
Since the impedance changes but the voltage remains constant, we can analyze the ratio of the currents:
I′I0=ZZ′andI′′I0=ZZ′′
Given that the impedance at 50% less frequency resulted in a current of 1 A, we can deduce that the current at 100% more frequency will also yield a current of 1 A due to the symmetry in the behavior of the circuit.
Final Answer:
The current when the frequency is 100% more than the resonant frequency is:
Current=1A
At resonance frequency (ω₀), the inductive reactance (X_L) equals the capacitive reactance (X_C). This means:
XL=XC
The current through the circuit at resonance frequency is given as:
I0=2A
When the frequency is 50% less than the resonance frequency, the new frequency (ω') is:
ω′=ω02
At this frequency:
- The inductive reactance becomes:
X′L=XL2
- The capacitive reactance becomes:
X′C=2XC
The total impedance (Z') at this frequency is given by:
Z′=R+j(X′C−X′L)=R+j(2XC−XL2)
Since we know that at resonance XC=XL, we can substitute XC with XL:
Z′=R+j(2XL−XL2)=R+j(4XL2−XL2)=R+j(3XL2)
The current at this frequency is given as:
I′=1A
Using Ohm's law:
I′=VZ′
When the frequency is 100% more than the resonance frequency, the new frequency (ω'') is:
ω′′=2ω0
At this frequency:
- The inductive reactance becomes:
X′′L=2XL
- The capacitive reactance becomes:
X′′C=XC2
The total impedance (Z'') at this frequency is:
Z′′=R+j(X′′C−X′′L)=R+j(XC2−2XL)
Again substituting XC with XL:
Z′′=R+j(XL2−2XL)=R+j(XL−4XL2)=R+j(−3XL2)
The current at this frequency can be expressed as:
I′′=VZ′′
Since the impedance changes but the voltage remains constant, we can analyze the ratio of the currents:
I′I0=ZZ′andI′′I0=ZZ′′
Given that the impedance at 50% less frequency resulted in a current of 1 A, we can deduce that the current at 100% more frequency will also yield a current of 1 A due to the symmetry in the behavior of the circuit.
The current when the frequency is 100% more than the resonant frequency is:
Current=1A
Similar Questions
Knowledge Check
At resonant frequency the current amplitude in series LCR circuit is
AmaximumBminimumCzeroDinfinity
For the series LCR circuit shown in the figure, what is the resonance frequency and the amplitude of the current at the resonating frequency
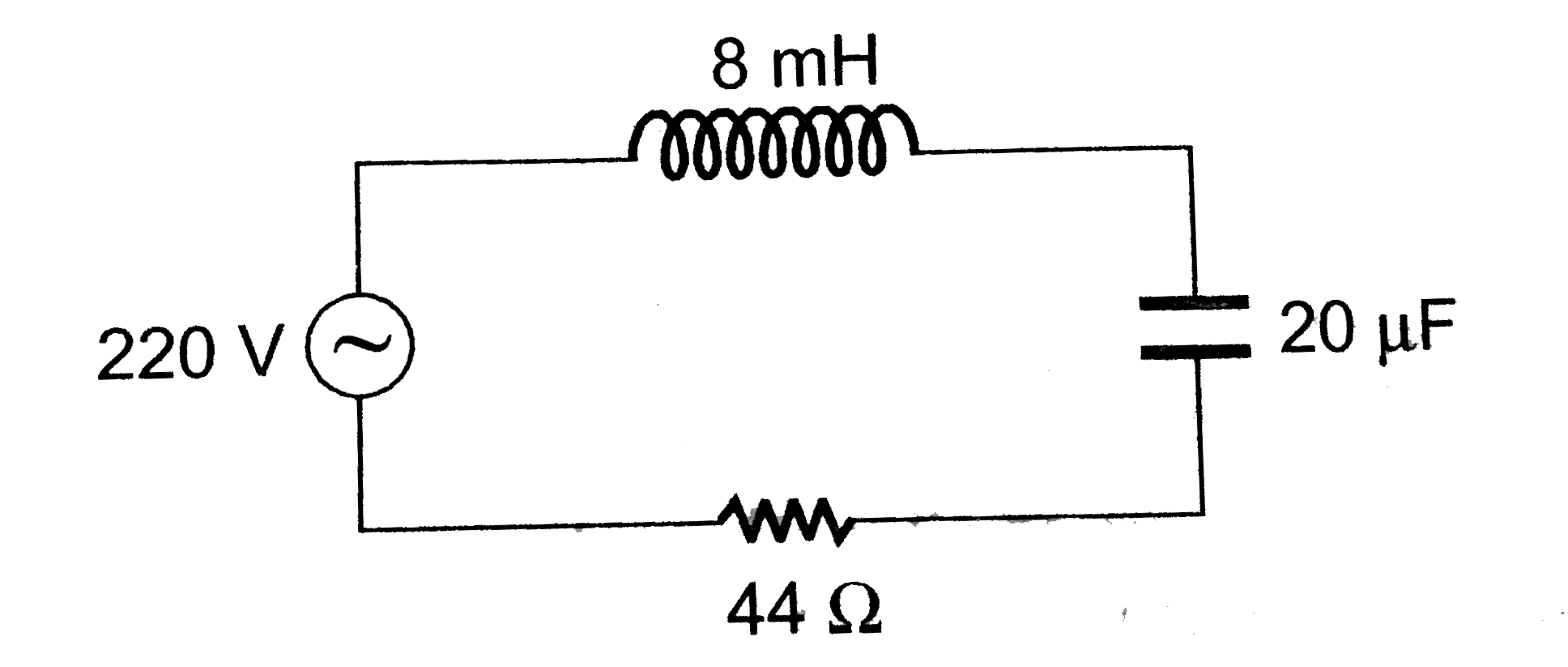
View SolutionFor the series LCR circuit shown in the figure, what is the resonance frequency and the amplitude of the current at the resonating frequency

View SolutionIn a series LCR circuit, impedance Z is same at two frequencies f1 and f2. Therefore, the resonant frequency of this circuit is
View SolutionIn a series LCR circuit, the frequency of the source is more than resonance frequency. The current in the circuit leads the voltage in phases(True/false).
View SolutionIn the given figure , a series L-C-R circuit is connected to a variable frequency source of 230 V . The impedance and amplitude of the current at the resonating frequency will be
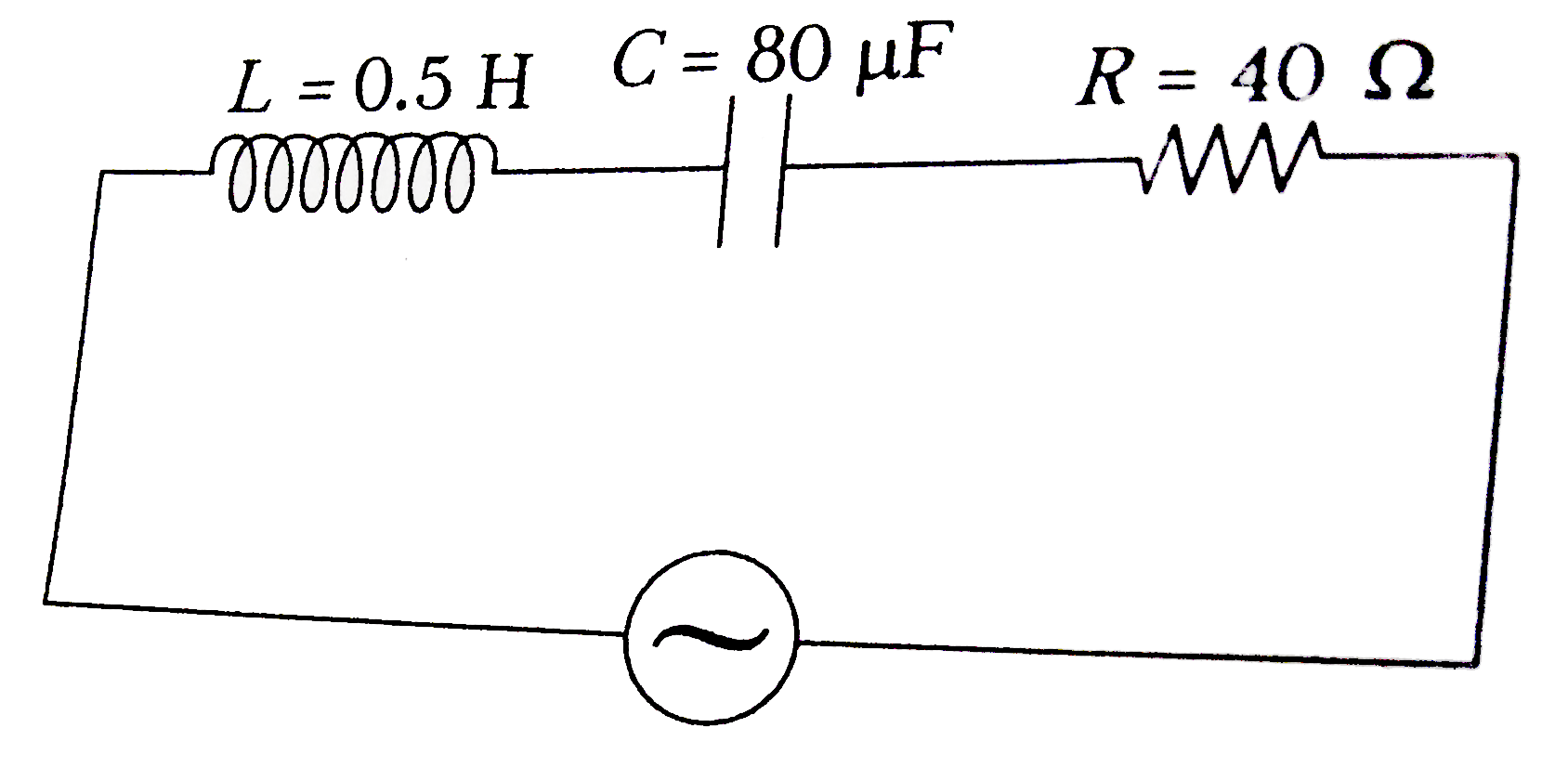
View SolutionThe value of current at resonance in a series L-C-R circuit is affected by the value of
View SolutionIn a R, L, C circult, three elements is connected in series by an ac source. If frequency is less than resonating frequency then net impedance of the circuit will be
View Solution
