The power factor of an R-L circuit is 1/√2 if the frequency of AC is doubled , what will be the power
1√3
1√5
1√7
1√11
The correct Answer is:B
To solve the problem step by step, we will analyze the given information about the R-L circuit, calculate the new power factor after the frequency is doubled, and derive the final result.
Step 1: Understand the given power factor
The power factor (PF) of the R-L circuit is given as cosϕ=1√2. This can be expressed in terms of resistance (R) and impedance (Z):
cosϕ=RZ
Thus, we can write:
Z=Rcosϕ=R1√2=R√2
Step 2: Relate impedance to resistance and inductive reactance
The impedance Z of an R-L circuit is also defined as:
Z=√R2+X2L
where XL is the inductive reactance given by XL=ωL=2πfL. From the previous step, we have:
R√2=√R2+X2L
Squaring both sides gives:
2R2=R2+X2L
This simplifies to:
X2L=R2⟹XL=R
Step 3: Determine the new inductive reactance when frequency is doubled
If the frequency f is doubled, the new inductive reactance X′L can be calculated as:
X′L=ω′L=2π(2f)L=2XL
Since we found that XL=R, we have:
X′L=2R
Step 4: Calculate the new impedance
Now we can find the new impedance Z′:
Z′=√R2+(X′L)2=√R2+(2R)2=√R2+4R2=√5R2=R√5
Step 5: Find the new power factor
The new power factor cosϕ′ can now be calculated:
cosϕ′=RZ′=RR√5=1√5
Final Answer
Thus, the new power factor when the frequency is doubled is:
cosϕ′=1√5
The power factor (PF) of the R-L circuit is given as cosϕ=1√2. This can be expressed in terms of resistance (R) and impedance (Z):
cosϕ=RZ
Thus, we can write:
Z=Rcosϕ=R1√2=R√2
The impedance Z of an R-L circuit is also defined as:
Z=√R2+X2L
where XL is the inductive reactance given by XL=ωL=2πfL. From the previous step, we have:
R√2=√R2+X2L
Squaring both sides gives:
2R2=R2+X2L
This simplifies to:
X2L=R2⟹XL=R
If the frequency f is doubled, the new inductive reactance X′L can be calculated as:
X′L=ω′L=2π(2f)L=2XL
Since we found that XL=R, we have:
X′L=2R
Now we can find the new impedance Z′:
Z′=√R2+(X′L)2=√R2+(2R)2=√R2+4R2=√5R2=R√5
The new power factor cosϕ′ can now be calculated:
cosϕ′=RZ′=RR√5=1√5
Thus, the new power factor when the frequency is doubled is:
cosϕ′=1√5
Similar Questions
Knowledge Check
The power factor of the circuit as shown in figure is
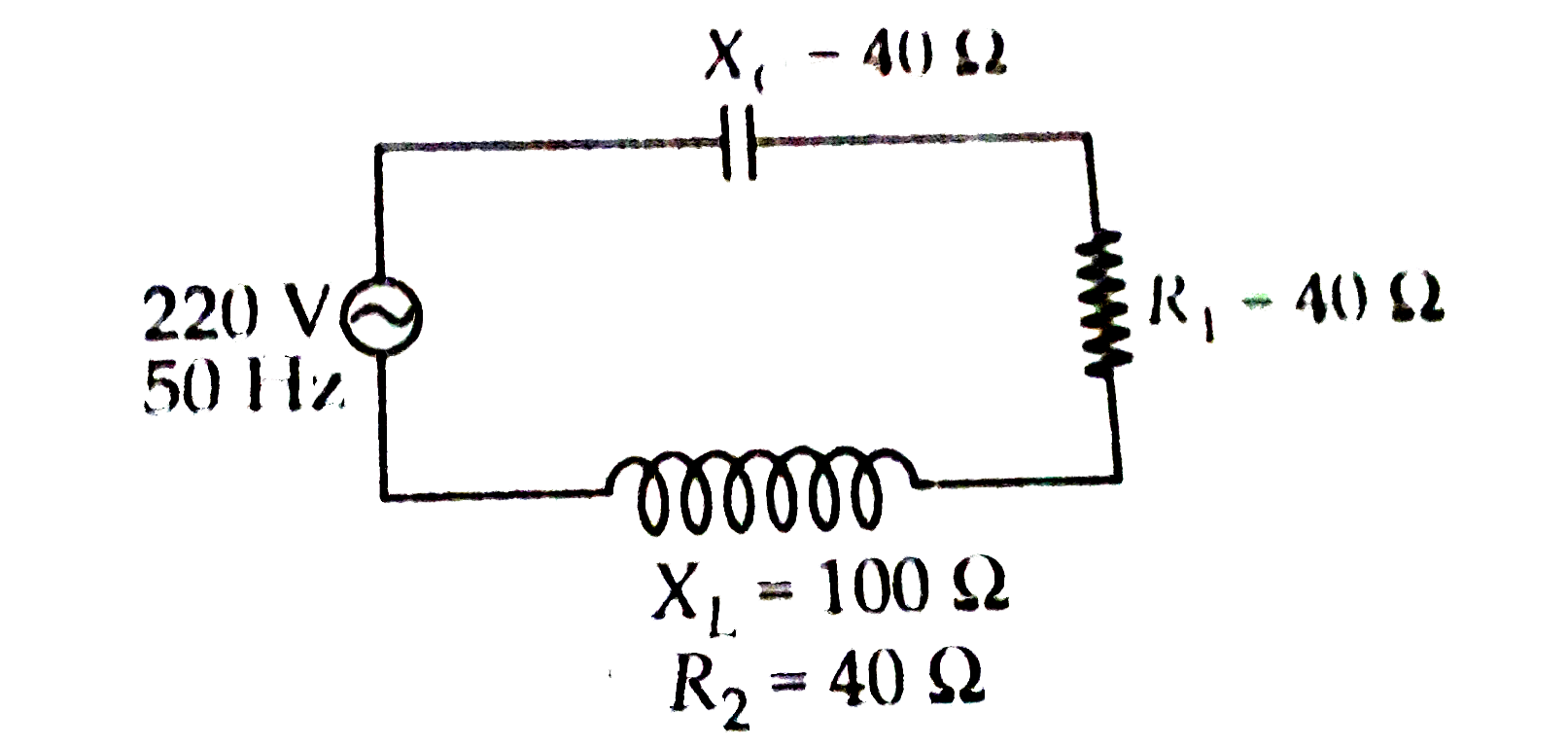 A0.2B0.4C0.8D0.6
A0.2B0.4C0.8D0.6
The power factor of LCR circuit at resonance is-
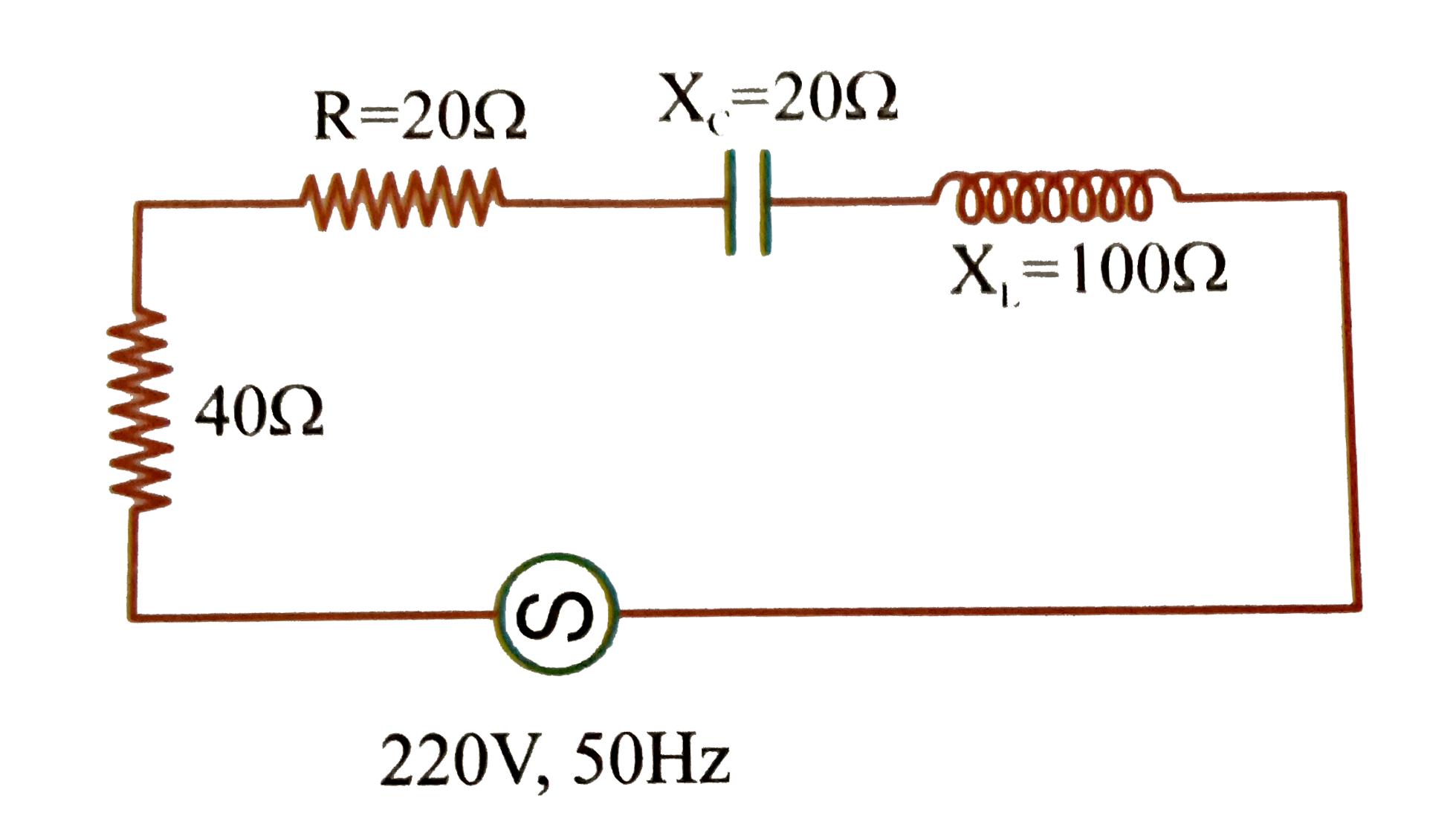
View SolutionPower factor of the circuit shown here is

View SolutionThe power factor of the following circuit will be
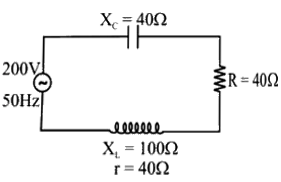
View SolutionThe power factor of the circuit shown in the figure is
View SolutionThe power factor of the circuit in fig. is 1/√2. The capacitance of the circuit is equal to
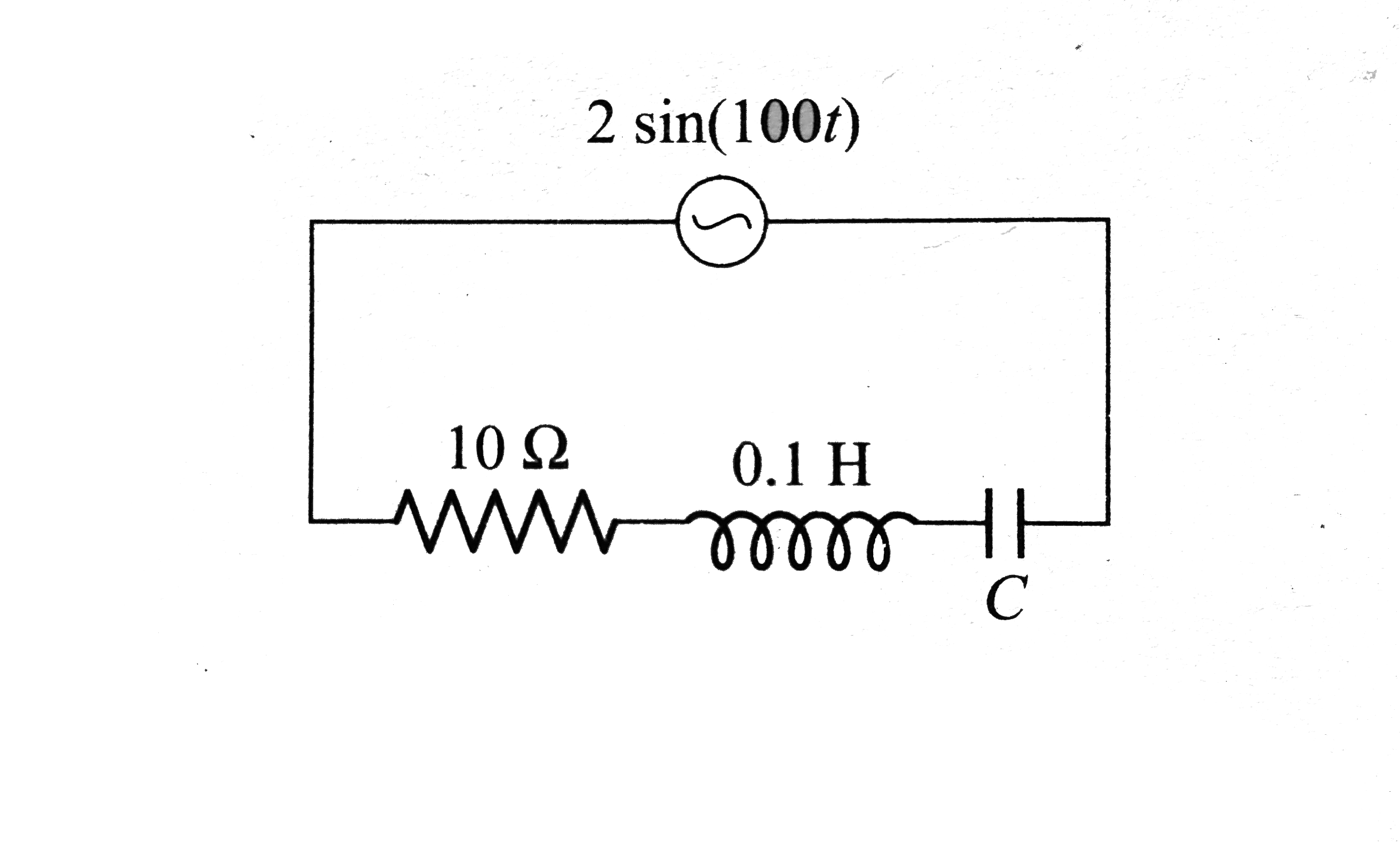
View SolutionWhat is the power factor for the circuit shown ?
View SolutionWhat is the power factor for the circuit shown ?

View Solution