Using an ac voltmeter, the potential difference in the electrical line in a house is read to be 234 V. If the line freqency is known to be 50 cycles per second, the equation for the line voltage is
165 sin (200πt)
234 sin (100πt)
331 sin (100πt)
440 sin (200πt)
The correct Answer is:C
To derive the equation for the line voltage based on the given information, we will follow these steps:
Step 1: Identify the given values
- The RMS voltage (V_RMS) is given as 234 V.
- The frequency (f) is given as 50 Hz.
Step 2: Calculate the peak voltage (V_0)
The relationship between the RMS voltage and the peak voltage is given by the formula:
VRMS=V0√2
Rearranging this formula to find the peak voltage (V_0):
V0=VRMS×√2
Substituting the given RMS voltage:
V0=234×√2
Calculating this gives:
V0≈234×1.414≈331 V
Step 3: Calculate the angular frequency (ω)
The angular frequency (ω) is related to the frequency (f) by the formula:
ω=2πf
Substituting the given frequency:
ω=2π×50=100π rad/s
Step 4: Write the equation for the line voltage
The general equation for an AC voltage can be expressed as:
V(t)=V0sin(ωt)
Substituting the values of V_0 and ω:
V(t)=331sin(100πt)
Final Equation
Thus, the equation for the line voltage is:
V(t)=331sin(100πt)
---
- The RMS voltage (V_RMS) is given as 234 V.
- The frequency (f) is given as 50 Hz.
The relationship between the RMS voltage and the peak voltage is given by the formula:
VRMS=V0√2
Rearranging this formula to find the peak voltage (V_0):
V0=VRMS×√2
Substituting the given RMS voltage:
V0=234×√2
Calculating this gives:
V0≈234×1.414≈331 V
The angular frequency (ω) is related to the frequency (f) by the formula:
ω=2πf
Substituting the given frequency:
ω=2π×50=100π rad/s
The general equation for an AC voltage can be expressed as:
V(t)=V0sin(ωt)
Substituting the values of V_0 and ω:
V(t)=331sin(100πt)
Thus, the equation for the line voltage is:
V(t)=331sin(100πt)
Similar Questions
A voltmeter reads the potential difference across the terminals of an old battery as 1.40V, while a potentiometer reads its voltage to be 1.55V. The voltmeter resistance is 280Ω.
View SolutionThe electric mains in a house are marked 220V-50Hz. Write down the equation for instantaneous voltage.
View SolutionIn a Coolidge tube, the potential difference used to accelerate the electrons is increased from 12.4kV to 24.8kV. As a result, the difference between the wavelengths of Kα-line and minimum wavelength becomes thrice. The wavelength of the Kα line is 0.25×KA∘. Find the value of K. hce=(12.4KVA∘)
View SolutionIn a Coolidge tube, the potential difference used to accelerate the electrons is increased from 24. 8 kV to 49.6 kV . As a result, the difference between the wavelength of Kα -line and minimum wavelength becomes two times. The initial wavelength of the Kα line is [Take hce=12.4kVÅ]
View Solution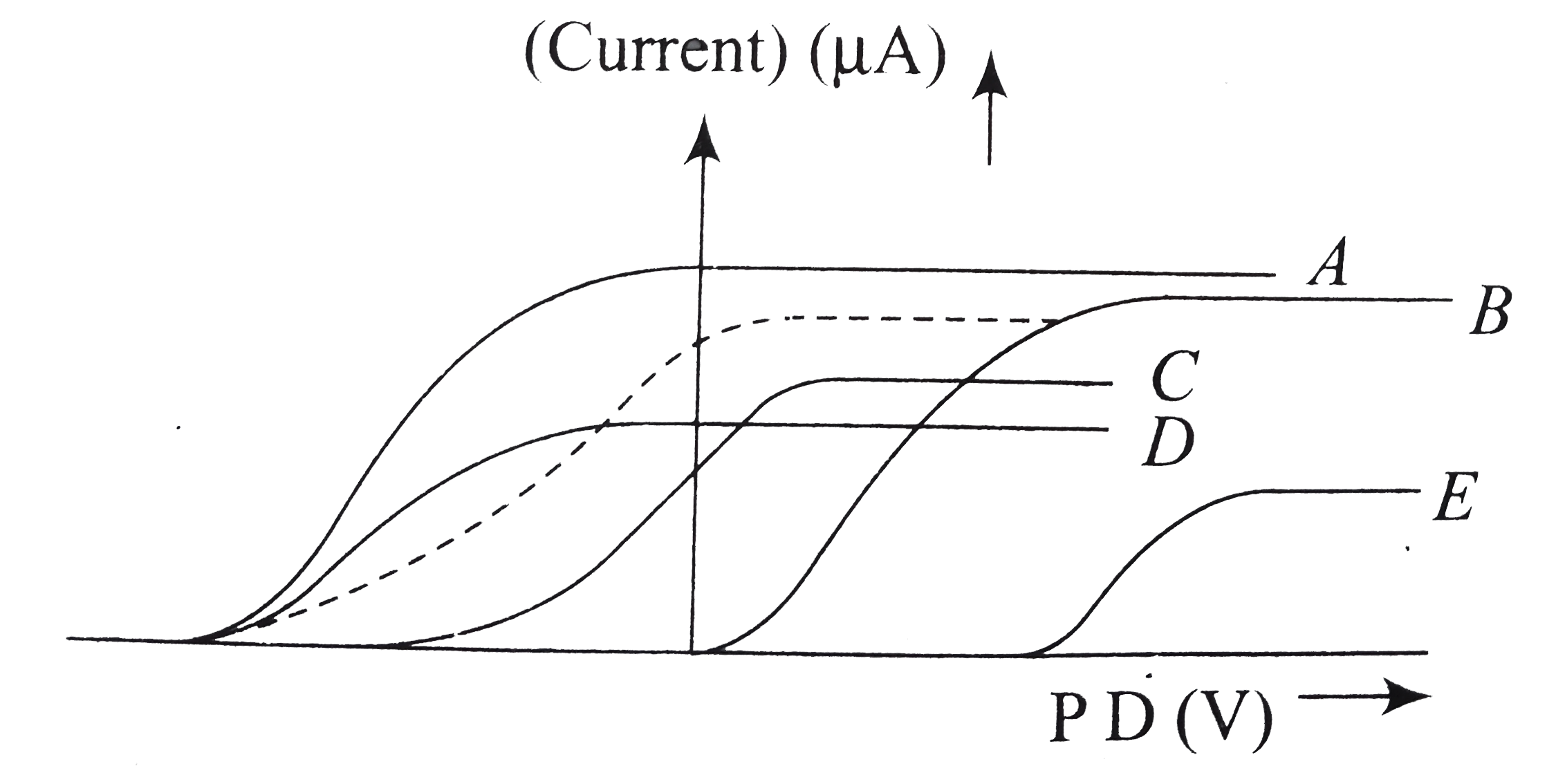
A photoelectric cell is connected to a source of variable potential difference, connected across it and the photoelectric current resulting (μA) is plotted against the applied potential difference (V). The graph in the broken line represents one for a given frequency and intensity of the incident radiation . If the frequency is increased and the intensity is reduced, which of the following graphs of unbroken line represents the new situation?
View SolutionAn electric iron is rated "220 V, 1 kW'. Under normal working conditions, find :
the power consumed if the line voltage falls to 180 V.
View SolutionAn electron of mass 'm' is accelerated through a potential difference of V and then it enters a magnetic field of inductionB. Normal to the lines of force. Then the radius of the circular path is
View SolutionThe instantaneous voltages at three terminals marked X, Y and Z are given by
VX=V0sinωt,VY=V0sin(ωt=2π3)andVz=V0sin(ωt=4π3)
An ideal voltmeter is configured to read runs value of the potential difference between its terminals. is connected between points X and Y and then between Y and Z. The reading the voltmeter will be
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionIn a series LCR circuit with an AC source, R=300Ω,C=20μF,L=1.0henry,εrms=50V and v=50πHz. Find (a) the rms current in the circuit and (b) the rms potential differences across the capacitor, the resistor and the inductor. Note that the sum of the rms potential differences across the three elements is greater than the rms voltage of the source.
View Solution
