Two coils have a mutual inductance 0.005 H. The alternating current changes in the first coil according to equation I = Iosinωt, where Io = 10 A and ω = 100π rads−1. The maximum value of emf in the second coil
is (in volt)
2π
5π
π
4π
The correct Answer is:B
To solve the problem, we need to find the maximum value of the induced electromotive force (emf) in the second coil due to the alternating current in the first coil. We will use the concept of mutual inductance and the formula for induced emf.
1. Identify the Given Values:
- Mutual inductance M=0.005H
- Current in the first coil I(t)=I0sin(ωt)
- Maximum current I0=10A
- Angular frequency ω=100πrad/s
2. Differentiate the Current:
- The induced emf in the second coil is given by the formula:
emf=−MdI1dt
- First, we need to differentiate the current I(t):
I(t)=I0sin(ωt)
dIdt=I0ωcos(ωt)
3. Substitute the Values:
- Substitute I0 and ω into the differentiation result:
dIdt=10⋅(100π)cos(100πt)=1000πcos(100πt)
4. Calculate the Induced emf:
- Now substitute dIdt into the emf formula:
emf=−MdIdt=−0.005⋅(1000πcos(100πt))
emf=−5πcos(100πt)
5. Determine the Maximum Value of emf:
- The maximum value of cos(100πt) is 1, hence:
Maximum emf=5πV
Final Answer:
The maximum value of the induced emf in the second coil is 5πV.
- Mutual inductance M=0.005H
- Current in the first coil I(t)=I0sin(ωt)
- Maximum current I0=10A
- Angular frequency ω=100πrad/s
- The induced emf in the second coil is given by the formula:
emf=−MdI1dt
- First, we need to differentiate the current I(t):
I(t)=I0sin(ωt)
dIdt=I0ωcos(ωt)
- Substitute I0 and ω into the differentiation result:
dIdt=10⋅(100π)cos(100πt)=1000πcos(100πt)
- Now substitute dIdt into the emf formula:
emf=−MdIdt=−0.005⋅(1000πcos(100πt))
emf=−5πcos(100πt)
- The maximum value of cos(100πt) is 1, hence:
Maximum emf=5πV
The maximum value of the induced emf in the second coil is 5πV.
Similar Questions
Two coils have a mutual inductance 0.005H. The current changes in the first coil according to the equation I=I0sinωtwhereI0=10Aandω=100πrad/s . The maximum value of emf wiin second coil is (pi//x) volts. Find the value of x.
View SolutionTwo coils have a mutual inductance 0.005H. The current changes in the first coil according to equation I=I0sinωt, where I0=10A and ω=100πradian//sec. The maximum value of e.m.f. in the second coil is
View SolutionTwo coils have a mutual inductance 0.005H. The current changes in the first coil according to equation I=I0sinωt, where I0=10A and ω=100π radian/sec. The maximum value of e.m.f. in the second coil is
View SolutionTwo coils have a mutual inductance of 0.005H. the current changes in the first coil according to equation I=I0sinωt, where I0=10A and ω=100πrad/s. The maximum value of emf (in volt) in the second coil is
View SolutionTwo coils have the mutual inductance of 0.05 H. The current changes in the first coil as I=I0sinωt, where I0=1A and ω=100πrad/s. The maximum emf induced in secondary coil is
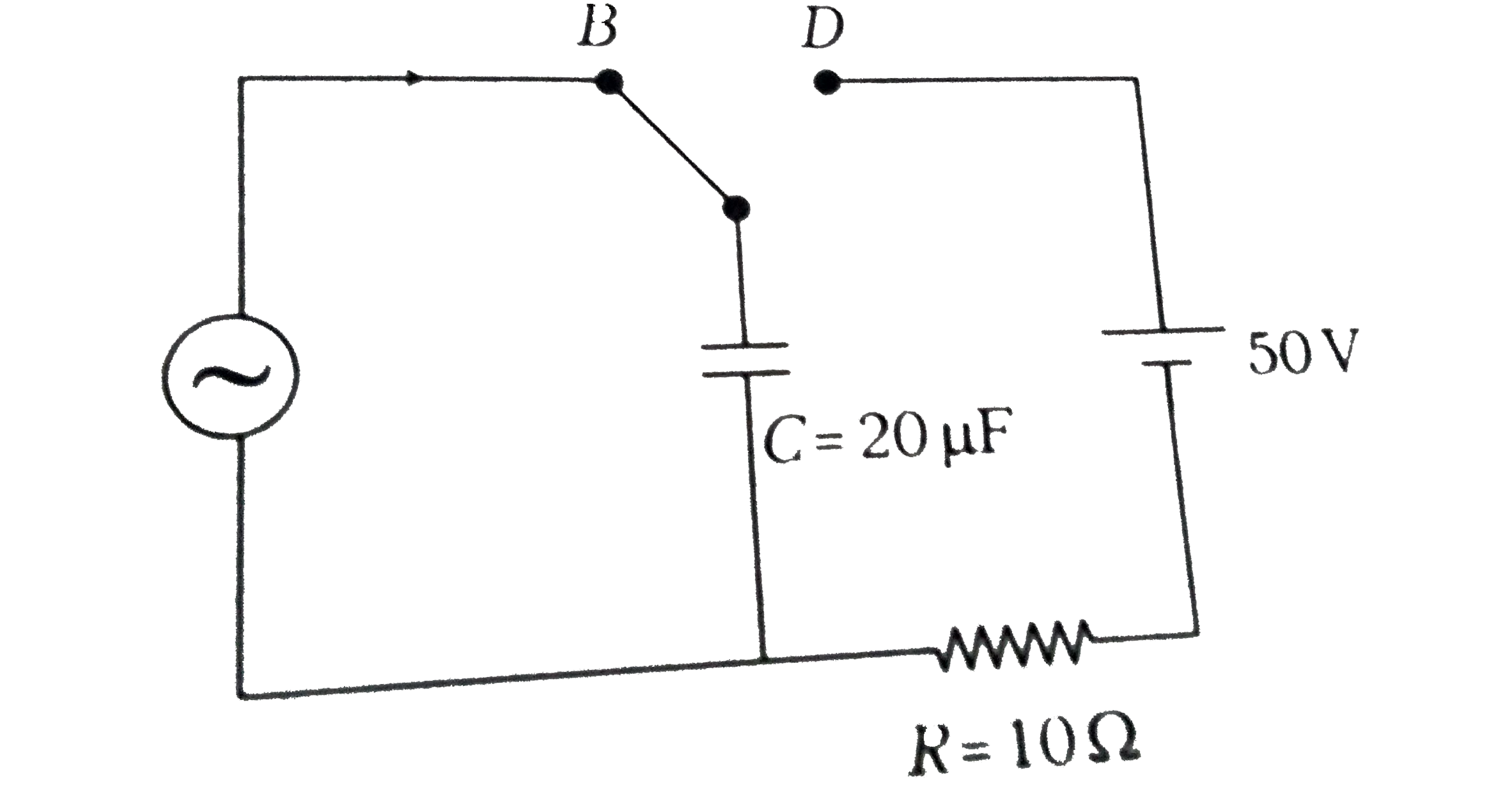
View SolutionAt time t = 0 , terminal A in the circuit shown in the figure is connected to B by a key and alternating current I(t) = Iocos(ωt), with Io = 1 A and ω = 500 rads−1 starts flowing in it with the initial direction shown in the figure . At t = 7π/6ω , the keys is switched from B to D . Now onwards only A and D are connected . A total charge Q flows from the battery to charge the capacitor fully. If C = 20 μ , R = 10 Ω and the battery is deal with emf of 50 V , identify the correct statement(s).
View SolutionCurrent and voltage in AC are I = Io sin (ωt + π/4) and V = Vo sin (ωt - π/4), Then
View SolutionTwo coils have mutual inductance M=3.25×104H. The current i1 in the ffrst coil increases at a uniform rate of 830A/s.
(a) What is the magnitude of the induced emf in the second coil? Is it constant?
(b) Suppose that the current described is in the second coil rather than the first. What is the induced emf in the first coil?
View SolutionA coil has a self inductance of 0.01H. The current through it is allowed to change at the rate of 1A in 10−2s . Calculate the emf induced.
View SolutionTwo coil A and B have coefficient of mutual inductance M=2H. The magnetic flux passing through coil A charges by 4 Weber in 10 seconds due to the change in current in B. Then
View Solution