If an 8Ω resistance and 6Ω reactance are present in an AC series circuit then the impedence of the circuit will be
2Ω
14Ω
4Ω
10Ω
The correct Answer is:D
To find the impedance of an AC series circuit with a given resistance and reactance, we can use the formula for impedance Z:
Z=√R2+X2
Where:
- R is the resistance (in ohms)
- X is the reactance (in ohms)
1. Identify the given values:
- Resistance R=8Ω
- Reactance X=6Ω
2. Substitute the values into the impedance formula:
Z=√R2+X2=√82+62
3. Calculate R2 and X2:
- R2=82=64
- X2=62=36
4. Add R2 and X2:
R2+X2=64+36=100
5. Take the square root:
Z=√100=10Ω
6. Conclusion:
The impedance of the circuit is Z=10Ω.
Final Answer:
The impedance of the circuit is 10Ω.
---
- R is the resistance (in ohms)
- X is the reactance (in ohms)
- Resistance R=8Ω
- Reactance X=6Ω
Z=√R2+X2=√82+62
- R2=82=64
- X2=62=36
R2+X2=64+36=100
Z=√100=10Ω
The impedance of the circuit is Z=10Ω.
The impedance of the circuit is 10Ω.
Similar Questions
Knowledge Check
In the series LCR circuit shown the impedance is
 A200ΩB100ΩC300ΩD500Ω
A200ΩB100ΩC300ΩD500ΩTwo 2Ω resistances are connected in parallel in the circuit X and in series in circuit Y. The batteries in the two circuits are identical and have zero internal resistance. Assume that the energy transferred to resistor A in circuit X within a certain time is W. The energy transferred to resistor B in circuit Y in the same time will be
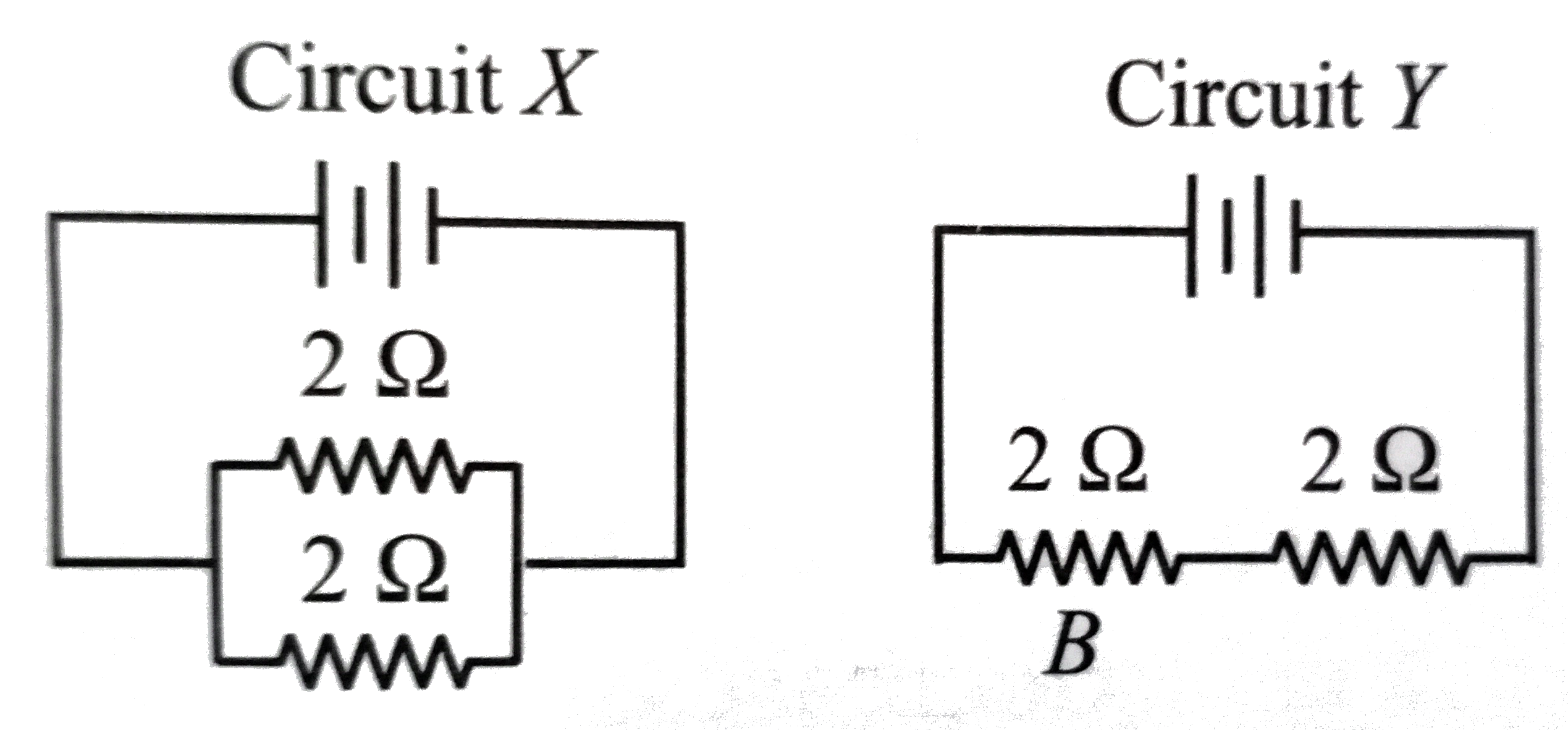 A14WB12WC2WD4W
A14WB12WC2WD4W
If both the resistance and the inductance in an LR AC series circuit are doubled the new impedance will be
View SolutionWhen the frequency of AC is doubled, the impedance of an LCR series circuit
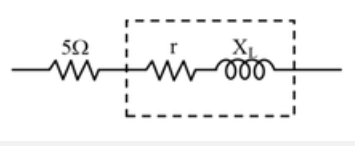
View SolutionThe current through an inductor of impedance 10Ω lags behind the voltage by a phase of 60∘ when just the inductor is connected to the ac source. Now the inductor is connected to a 5Ω resistance in series, then the net impedance of the circuit is
View SolutionA series AC circuit has a resistance of 4Ω and a reactance of 3Ω. The impedance of the circuit is
View SolutionA series AC circuit has a resistance of 4Ω and a reactance of 3Ω. The impedance of the circuit is
View SolutionAn AC of frequency f is flowing in a circuit containing a resistance R and capacitance C in series. The impedance of the circuit is equal to
View Solution

