The frequency of the sinusoidal wave
y=0.40cos[2000t+0.80x] would be
1000 Hz
2000 Hz
20 Hz
1000 / π Hz
The correct Answer is:D
To find the frequency of the sinusoidal wave given by the equation y=0.40cos(2000t+0.80x), we can follow these steps:
Step 1: Identify the angular frequency (ω)
The general form of a sinusoidal wave is given by:
y=Acos(ωt+kx+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- k is the wave number,
- ϕ is the phase constant.
From the given equation y=0.40cos(2000t+0.80x), we can see that:
ω=2000rad/s
Step 2: Relate angular frequency to frequency (f)
The relationship between angular frequency ω and frequency f is given by the formula:
ω=2πf
Step 3: Solve for frequency (f)
We can rearrange the formula to solve for f:
f=ω2π
Substituting the value of ω:
f=20002π
f=1000πHz
Step 4: Conclusion
Thus, the frequency of the sinusoidal wave is:
f=1000πHz
Final Answer
The frequency of the sinusoidal wave is 1000π Hz.
---
The general form of a sinusoidal wave is given by:
y=Acos(ωt+kx+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- k is the wave number,
- ϕ is the phase constant.
ω=2000rad/s
The relationship between angular frequency ω and frequency f is given by the formula:
ω=2πf
We can rearrange the formula to solve for f:
f=ω2π
f=20002π
f=1000πHz
Thus, the frequency of the sinusoidal wave is:
f=1000πHz
The frequency of the sinusoidal wave is 1000π Hz.
Similar Questions
If the equation of a travelling wave is given as y = 40 cos (1600t + 6x), (where y is in millimeter, t is in second and x is in meter), then ratio of the wave speed to the maximum particle speed will be
View SolutionThe equation of a progressive wave is
y=0.02sin2π[t0.01−x0.30]
here x and y are in metres and t is in seconds. The velocity of propagation of the wave is
View Solution
Knowledge Check
Figure given shows a sinusoidal wave on a string. If the frequency of the wave is 150 Hz, what is the velocity and wavelength of the given wave?
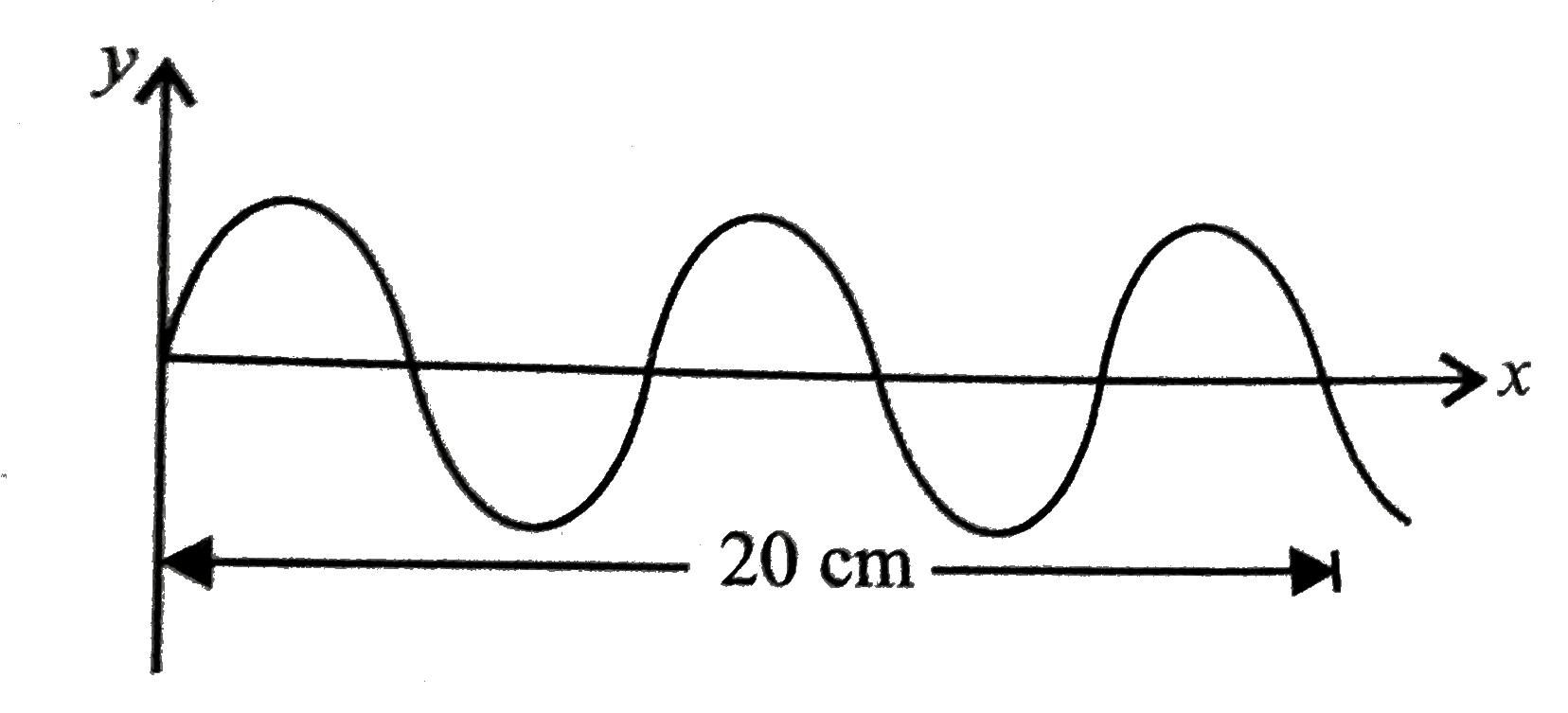 A0.04m,10ms−1B0.06m,12ms−1C0.08m,10ms−1D0.08m,12ms−1
A0.04m,10ms−1B0.06m,12ms−1C0.08m,10ms−1D0.08m,12ms−1
The equation of a transverse wave is given by
y=10sinπ(0.01x−2t)
where x and y are in cm and t is in second. Its frequency is
View SolutionThe equation of a simple harmonic motion is X=0.34cos(3000t+0.74) where X and t are in mm and sec . The frequency of motion is
View SolutionThe equations for two sinusoidal waves propagating through a string are given by, y1=4sin(20x−30t)
y2=4sin(25−x−40t)
where y and x are in centimeters and t is second.
(i) What is the phase difference between these two waves at the points x=5.0 cm and at t=2.0 s?
(ii) When these two waves interface what is the maximum and minimum value of the intensity?
View SolutionDetermine the amplitudes of the resultant motion when two sinusoidal waves of same frequency , travelling in the same direction are combined . Their amplitudes are 3.0cmand4.0cm and they differ in phase by π/2radians.
View SolutionThe equation of a travelling wave is
y(x,t)=0.02sin(x0.05+t0.01)m
Find (a) the wave velocity and
(b) the particle velocity at x=0.2mandt=0.3s.
Given cosθ=−0.85, where θ=34rad
View SolutionThe equation of a travelling wave is
y(x,t)=0.02sin(x0.05+t0.01)m
Find (a) the wave velocity and
(b) the particle velocity at x=0.2mandt=0.3s.
View SolutionThe equation of a sound wave is y=0.0015sin(62.4x+316t) the wavelength of this wave is
View Solution
