An L-C circuit contains 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant the circuit is closed be t = 0. what is the total energy stored initially ? At what times is the total energy shared equally between the inductor and the capacitor ?
To solve the problem step by step, we will first calculate the total energy stored initially in the LC circuit and then find the times when the energy is shared equally between the inductor and the capacitor.
Step 1: Calculate the initial total energy stored in the LC circuit.
The formula for the energy stored in a capacitor is given by:
E=12Q2C
Where:
- E is the energy,
- Q is the charge on the capacitor,
- C is the capacitance.
Given:
- Q=10mC=10×10−3C
- C=50μF=50×10−6F
Substituting the values into the formula:
E=12(10×10−3)250×10−6
Calculating the numerator:
(10×10−3)2=100×10−6=1×10−4
Now substituting this back into the energy formula:
E=121×10−450×10−6=121×10−450×10−6=1×10−4100×10−6=1100=0.01J
Thus, the total energy stored initially is:
E=1J
Step 2: Determine the times when the total energy is shared equally between the inductor and the capacitor.
When the energy is equally shared, the energy in the capacitor EC is equal to the energy in the inductor EL. The total energy E is given by:
E=EC+EL
Since EC=EL, we have:
E=2EC⟹EC=E2
The energy stored in the capacitor at any time t is given by:
EC=12Q2C
At the time when the energy is equally shared, we can express the charge on the capacitor as:
Q′=Qcos(ωt)
Where ω=1√LC is the angular frequency of the LC circuit.
Substituting Q′ into the energy formula:
EC=12(Qcos(ωt))2C
Setting this equal to E2:
12(Qcos(ωt))2C=12⋅Q2C
This simplifies to:
(Qcos(ωt))2=12Q2
Taking the square root:
Qcos(ωt)=Q√2⟹cos(ωt)=1√2
The cosine function equals 1√2 at:
ωt=π4+2nπandωt=7π4+2nπ(n=0,1,2,…)
Now substituting ω=1√LC:
ω=1√20×10−3×50×10−6
Calculating LC:
LC=20×10−3×50×10−6=1×10−6⟹√LC=1×10−3
Thus:
ω=11×10−3=1000rad/s
Now, substituting back to find t:
1000t=π4⟹t=π4000
1000t=7π4⟹t=7π4000
Thus, the times when the energy is shared equally between the inductor and the capacitor are:
t=π4000,7π4000 and other values based on n.
Summary of the Solution:
1. The total energy stored initially in the circuit is 1J.
2. The times when the total energy is shared equally between the inductor and capacitor are t=π4000 and t=7π4000.
- E is the energy,
- Q is the charge on the capacitor,
- C is the capacitance.
- Q=10mC=10×10−3C
- C=50μF=50×10−6F
1000t=7π4⟹t=7π4000
2. The times when the total energy is shared equally between the inductor and capacitor are t=π4000 and t=7π4000.
Similar Questions
An LC circuit contains a 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant the circuit is closed be t = 0.
(a) What is the total energy stored initially ? Is it conserved during the oscillalions?
(b) What is the natural frequency of the circuit?
(c ) At what time is the energy stored? (i) Completely electrical ? (ii) Completely magnetic ?
(d) At what time is the total energy shared equally between the inductor and the capacitor ?
(e) If a resistor is inserted in the circuit, how much energy is eventually dissipated as heat ?
View SolutionAn L-C circuit contains a 0.60 H inductor and a 25μF capacitor. What is rate of change of current when the charges on the capacitor is3.0×10−5C?
View Solution
Knowledge Check
An LC circuit contains a 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant at which the circuit which is closed be t=0. At what time the energy stored is completely magnetic ?
At = 0Bt=1.54msCt=3.14msDt=6.28msAn LC circuit contains a 20 mH inductor and 25μF capacitor with an initial charge of 5 mC. The total energy stored in the circuit initially is
A5 JB0.5JC50 JD500 JAn Lc circuit contains a 40 mH inductor and a 25μF capacitor. The resistance of the circuit is negligible.The time is measured from the instant the circuit is closed. The energy stored in the circuit is completely magnetic at time (in milliseconds)
A0,3.14,6.28B0,1.57,4.71C1.57,4.71,7.85D1.57,3.14,4.71
An L−C circuit consists of a 20.0mH inductor and a 0.5μF capacitor. If the maximum instantaneous current is 0.1A, what is the greatest potential difference across the capacitor?
View SolutionA circuit containing an 80mH inductor and a 60μF capacitor in series is connected to a 230V−50Hz Supply. The resistance in the circuit is negligible .
(a) Obtain the current amplitude and rms currents.
(b) Obtain the rms values of voltage across inductor and capacitor.
(c ) What is the average power transferred to the inductor and to the capacitor?
(d) What is the total power absorbed by the circuit?
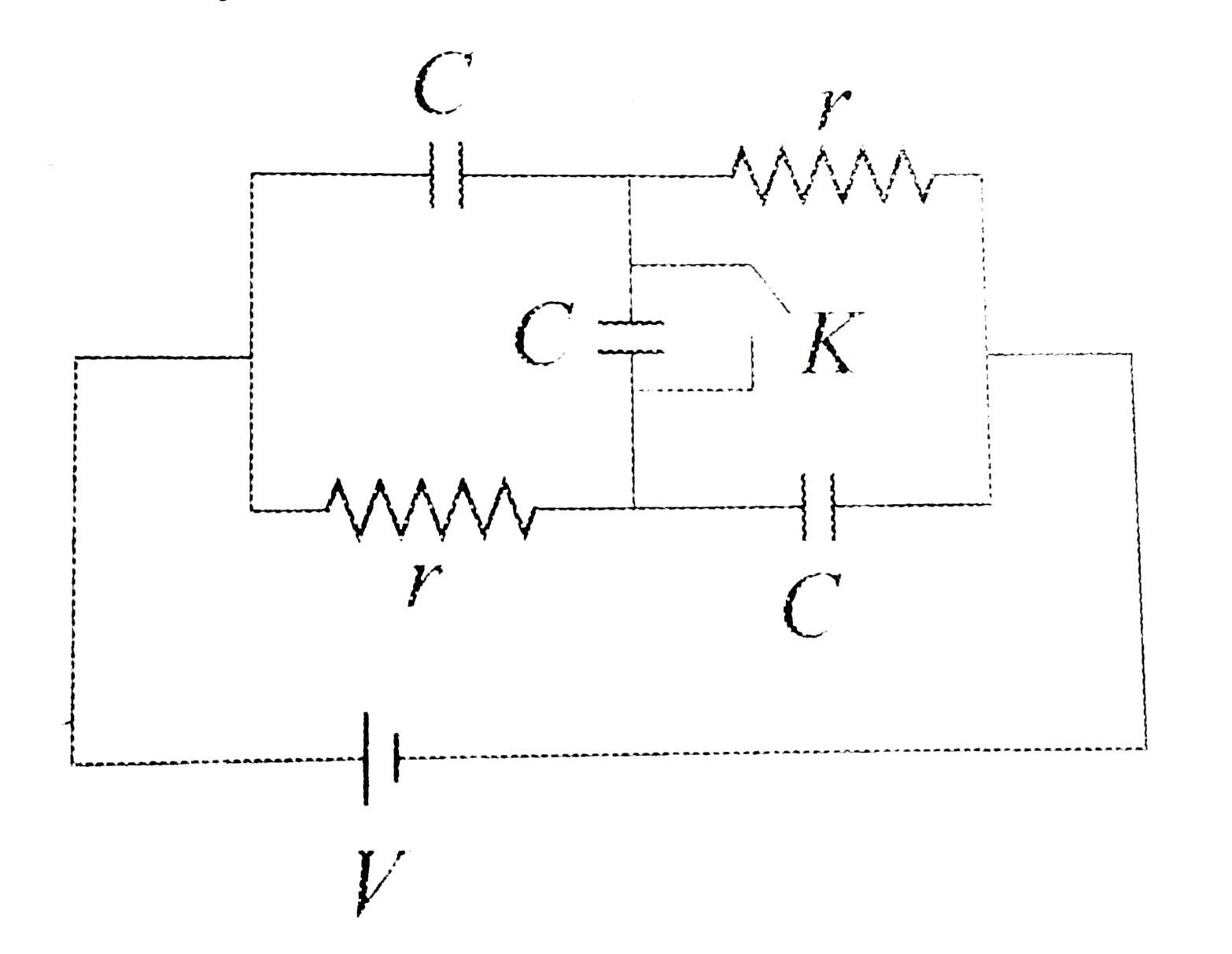
View SolutionIn the circuit what is the change of total electrical energy stored in the capacitors when the key is pressed ?
View SolutionThe circuit is switched on at t=0, Find the time when energy stored in inductor becomes 1n tiimes of maximum energy stored in it:
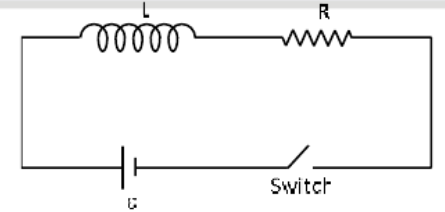
View SolutionThe circuit is switched on at t=0, Find the time when energy stored in inductor becomes 1n tiimes of maximum energy stored in it:

View Solution
