Inductance (L), capacitance (C) and resistance (R) are constained in a box. When 250 V DC is applied to the terminals of the box, a current of 1.0A floes in the circuit. When an AC source of 250Vrms at 2250radsec−1 is connected, a current of 1.25Arms flows. It is observed that the current rises with frequency and becomes maximum at 4500radsec−1. find the values of L,C and R. draw the circuit diagram.
When DC sources is applied, current = 1A
In DC circuit, inductor offers zero resistance and capacitor offer infinite resistance, R and C cannot be in series.
I=VrmsIrms=2501.25=200Ω
As Z<R, R L and C cannot be in series.
R cannot be in series with C as explained earlier.
As current is maximum at resonance and current increase with frequency, R cannot be in series with L. In fact, L and C must be in series.
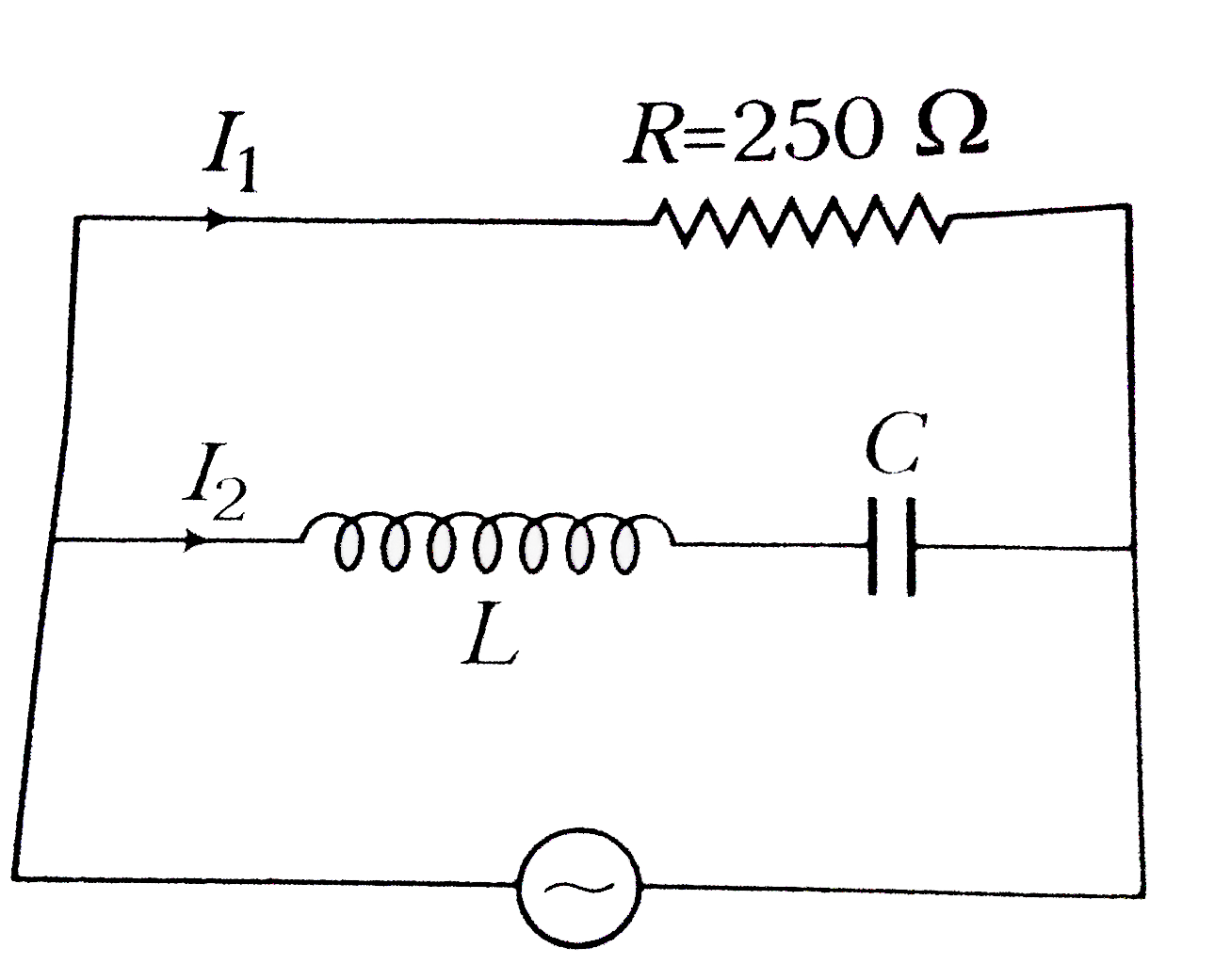
I1=250250=1A, in phase with voltage impedance of lower branch.
⇒Z′=∣∣∣(ωL−1ωC)∣∣∣
The phase difference between I2 and the voltage is π2
The angle between I1 and I2 is 90∘.
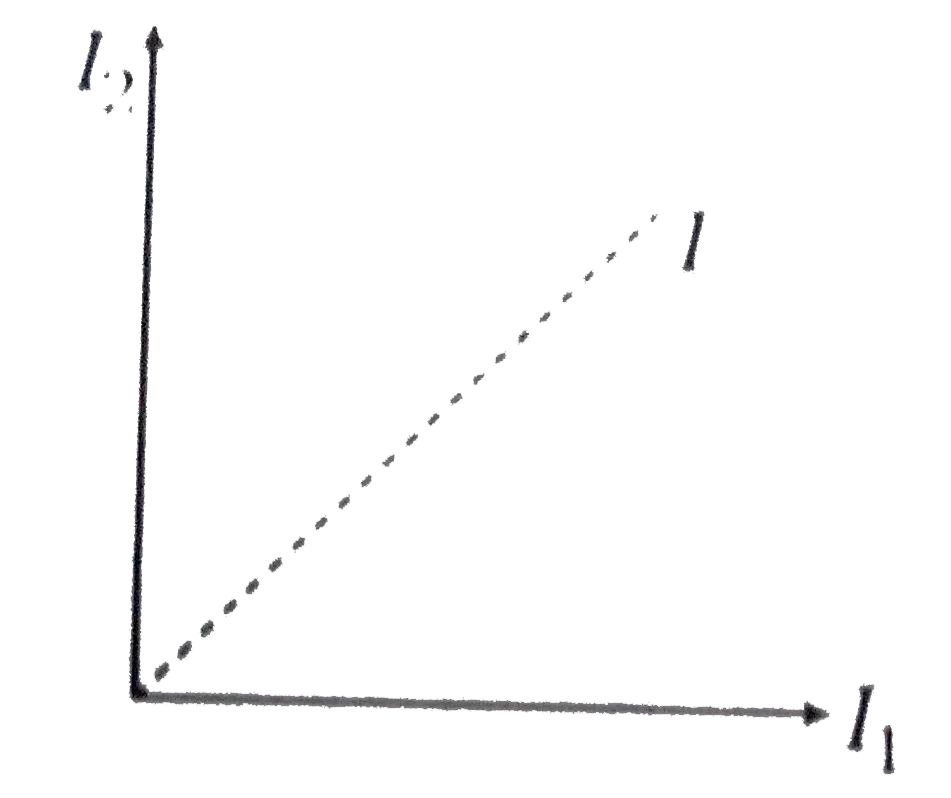
I21+I22=I2⇒(1)2+I22=(1.25)2
⇒I2=(1.25)2−(1)2=(2.25)(0.25)
⇒I2=1.5×0.5=0.75A
⇒I2=VZ′
∴Z′=VI2
⇒∣∣∣ωL−1ωC∣∣∣=0.250.75⇒∣∣∣ω2LC−1ωC∣∣∣=10003
⇒∣(2250)2LC−1)2250C∣10003..........(i)
At resosance, I2 is maximum, Z′ is minimum
⇒Z′=ωL−1ωC=0
⇒1LC=ω2=ω2r=(4500)2............(ii)
Similar Questions
Inductance (L), capacitance (C) and resistance (R) are connected in a box. When 250 V DC is applied to the terminals of the box, a current of 1.0A flows in the circuit. When an AC source of 250Vrms at 2250radsec−1 is connected, a current of 1.25Arms flows. It is observed that the current rises with frequency and becomes maximum at 4500radsec−1. Find the values of L,C and R. Draw the circuit diagram.
View SolutionA inductor of reactance 1Ω and a resistor of 2Ω are connected in series to the terminals of a 6 V (rms) a.c. source. The power dissipated in the circuit is
View Solution
Knowledge Check
A inductor of reactance 1Ω and a resistor of 2Ω are connected in series to the terminals of a 6 V (rms) a.c. source. The power dissipated in the circuit is
A8 WB12 WC14.4WD18 W
A inductor of reactance 1Ω and a resistor of 2Ω are connected in series to the terminals of a 6 V (rms) a.c. source. The power dissipated in the circuit is
View SolutionIn the circuit of fig, the source freqency is ω=2000rads−1. The current in the will be

View SolutionWhen 100 V dc is applied across a coil, a current of 1A flows through it and when 100 V ac of 50 Hz is applied to the same coil, only 0.5 flows
The inductance of coil is
View SolutionWhen 100V DC is applied across a solenoid, a current of 1.0A flows in it. When 100V AC is applied across the same coil. The current drops to 0.5A. If the frequency of the ac source is 50Hz, the impedance and inductance of the solenoid are
View SolutionWhen 100V DC is applied across a solenoid, a current of 1.0A flows in it. When 100V AC is applied across the same coil. The current drops to 0.5A. If the frequency of the ac source is 50Hz, the impedance and inductance of the solenoid are
View SolutionIn a series LCR circuit the rms voltage across the inductance , capacitance and resistance are respectively 4 V, 8 V and 5 V . The RMS voltage of the AC source in the circuit is
View SolutionA battery has e.m.f. 4 V and internal resistance r . When this battery is connected to an external resistance of 2 ohms , a current of 1 amp . flows in the circuit. How much current will flow if the terminals of the battery are connected directly
View Solution
