A circuit conatining of a capacitor and an active resistance R= connected in series is fed and alternating voltage with amplitude . In this case, the amplitude of current is equal to . Find the phase difference between the current and the voltage fed .
To find the phase difference between the current and the voltage in a circuit containing a capacitor and an active resistance connected in series, we can follow these steps:
Step 1: Identify the given values
- Resistance R=110Ω
- Amplitude of voltage V0=110V
- Amplitude of current I0=0.50A
Step 2: Use the relationship between current, voltage, and impedance
We know that the amplitude of the current is related to the amplitude of the voltage and the impedance Z by the formula:
I0=V0Z
Substituting the known values:
0.50=110Z
Step 3: Solve for impedance Z
Rearranging the equation to solve for Z:
Z=1100.50=220Ω
Step 4: Use the impedance formula for R and XC
The impedance in a series circuit with resistance R and capacitive reactance XC is given by:
Z=√R2+X2C
Substituting the known values:
220=√1102+X2C
Step 5: Square both sides to eliminate the square root
2202=1102+X2C
Calculating 2202 and 1102:
48400=12100+X2C
Step 6: Solve for X2C
X2C=48400−12100=36300
Step 7: Find XC
Taking the square root:
XC=√36300≈190.5Ω
Step 8: Calculate the phase difference ϕ
The phase difference ϕ can be found using:
tanϕ=XCR
Substituting the values:
tanϕ=190.5110
Step 9: Calculate ϕ
Calculating tanϕ:
tanϕ≈1.732
Now, finding ϕ:
ϕ=tan−1(1.732)≈60∘
Final Answer
The phase difference ϕ between the current and the voltage is approximately 60∘.
---
- Resistance R=110Ω
- Amplitude of voltage V0=110V
- Amplitude of current I0=0.50A
We know that the amplitude of the current is related to the amplitude of the voltage and the impedance Z by the formula:
I0=V0Z
Substituting the known values:
0.50=110Z
Rearranging the equation to solve for Z:
Z=1100.50=220Ω
The impedance in a series circuit with resistance R and capacitive reactance XC is given by:
Z=√R2+X2C
Substituting the known values:
220=√1102+X2C
2202=1102+X2C
Calculating 2202 and 1102:
48400=12100+X2C
X2C=48400−12100=36300
Taking the square root:
XC=√36300≈190.5Ω
The phase difference ϕ can be found using:
tanϕ=XCR
Substituting the values:
tanϕ=190.5110
Calculating tanϕ:
tanϕ≈1.732
Now, finding ϕ:
ϕ=tan−1(1.732)≈60∘
The phase difference ϕ between the current and the voltage is approximately 60∘.
Similar Questions
Find the phase difference between voltage and current in L-C circuit.
View SolutionThe phase difference between voltage and current in series L-C circuit is
View SolutionIn a series LCR circuit resistance R=10Ω and the impedance Z=10Ω The phase difference between the current and the voltage is
View SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
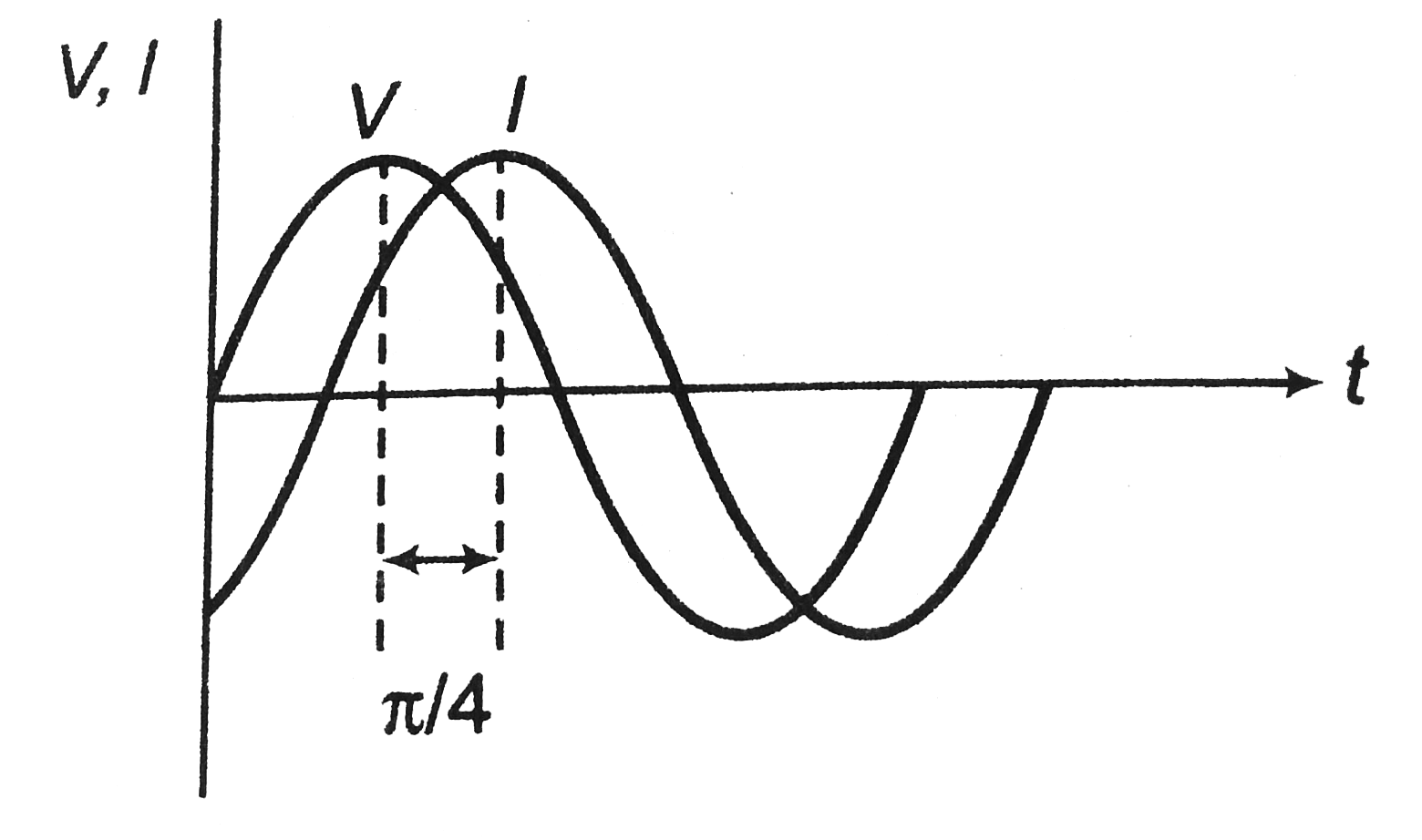 .
.
View SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
 .
.
View SolutionIn a series C−R circuit shown in figureure, the applied voltage is 10V and the voltage across capacitor is found to8V. The voltage across R, and the phase difference between current and the applied voltage will respectively be
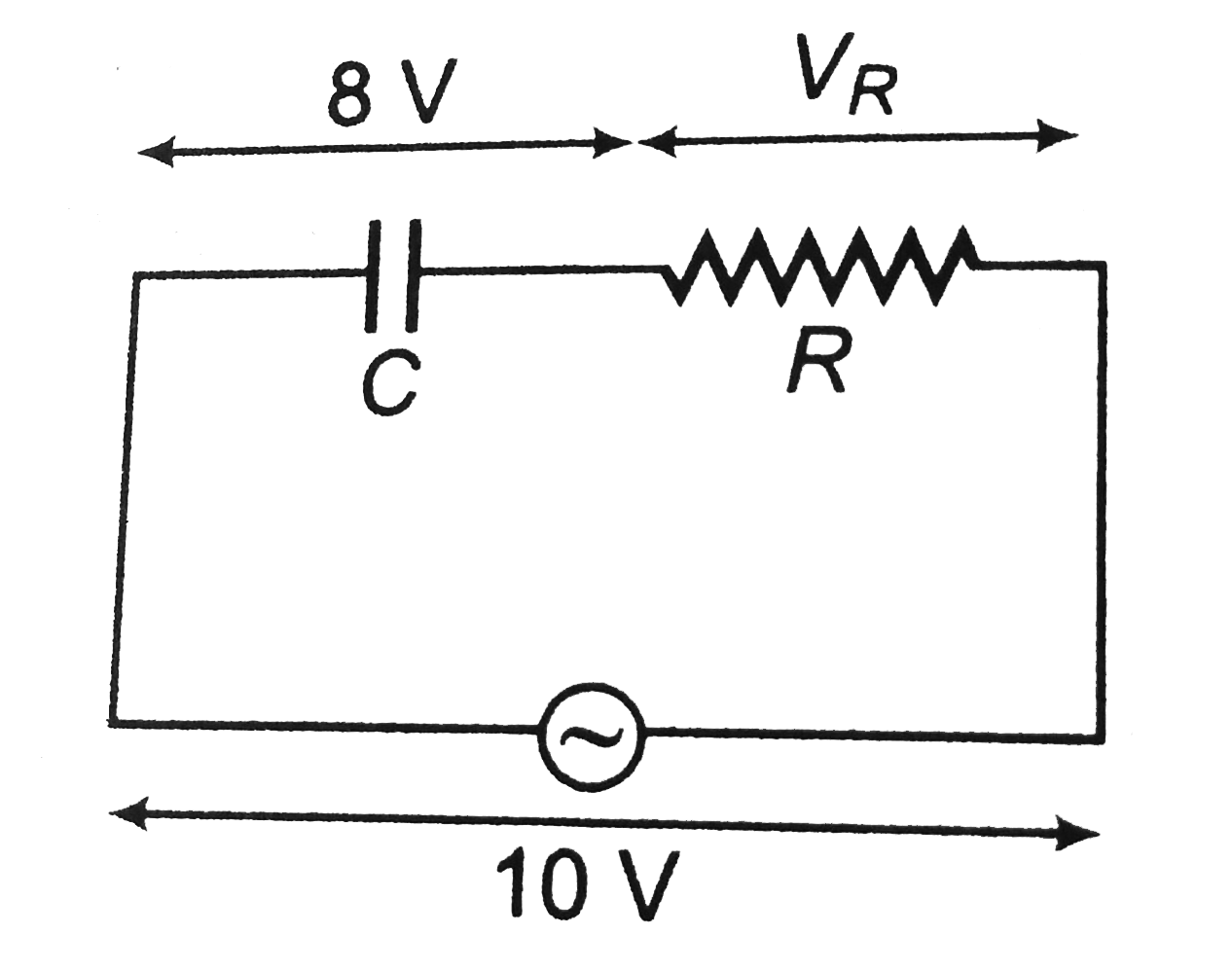 .
.
View SolutionIn a series C−R circuit shown in figureure, the applied voltage is 10V and the voltage across capacitor is found to8V. The voltage across R, and the phase difference between current and the applied voltage will respectively be
 .
.
View SolutionA 200Ω resistor is connected to a 220 V, 50 Hz AC supply. Calculate rms value of current in the circuit. Also find phase difference between voltage and the current.
View SolutionA capacitor of capacitance 100μF and a coil of resistance 50Ω and inductance 0.5H are connected in series with a110V,50HzAC source. Find the rms value of the current.
View SolutionA 0.21H inductor and a 12ohm resistance are connected in series to a 220V. 50Hz ac source. Calculate the current in the circuit and the phase angle between the current and the source voltage.
View Solution