Two liquids of densities 2ρ and ρ having their volumes in the ratio 3:2 are mixed together. Density of the mixture will be
2ρ3
ρ2
8ρ5
4ρ5
The correct Answer is:C
To find the density of the mixture of two liquids with given densities and volume ratios, we can follow these steps:
Step 1: Identify the given values
- Density of the first liquid, ρ1=2ρ
- Density of the second liquid, ρ2=ρ
- Volume ratio of the two liquids, V1:V2=3:2
Step 2: Express the volumes in terms of a common variable
Let the volume of the first liquid V1=3x and the volume of the second liquid V2=2x, where x is a common variable.
Step 3: Calculate the total mass of each liquid
- Mass of the first liquid, m1=ρ1×V1=(2ρ)×(3x)=6ρx
- Mass of the second liquid, m2=ρ2×V2=ρ×(2x)=2ρx
Step 4: Calculate the total mass of the mixture
Total mass of the mixture, mtotal=m1+m2=6ρx+2ρx=8ρx
Step 5: Calculate the total volume of the mixture
Total volume of the mixture, Vtotal=V1+V2=3x+2x=5x
Step 6: Calculate the density of the mixture
Density of the mixture, ρmixture=mtotalVtotal=8ρx5x=8ρ5
Final Answer
The density of the mixture is 8ρ5.
---
- Density of the first liquid, ρ1=2ρ
- Density of the second liquid, ρ2=ρ
- Volume ratio of the two liquids, V1:V2=3:2
Let the volume of the first liquid V1=3x and the volume of the second liquid V2=2x, where x is a common variable.
- Mass of the first liquid, m1=ρ1×V1=(2ρ)×(3x)=6ρx
- Mass of the second liquid, m2=ρ2×V2=ρ×(2x)=2ρx
Total mass of the mixture, mtotal=m1+m2=6ρx+2ρx=8ρx
Total volume of the mixture, Vtotal=V1+V2=3x+2x=5x
Density of the mixture, ρmixture=mtotalVtotal=8ρx5x=8ρ5
The density of the mixture is 8ρ5.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.2
10 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.3
10 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.35
1 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
If two liquids of same volume but different densities ρ1 and ρ2 are mixed, then the density of the mixture is:
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionEqual masses of water and a liquid of density 2g/cm3 are mixed together. The density of mixture is:
View SolutionTwo substances of densities ρ1 and ρ2 are mixed in equal volume and the relative density of mixture is 4. When they are mixed in equal masses, the relative density of the mixture is 3. the values of ρ1 and ρ2 are:
View SolutionEqual masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
View SolutionIf equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
View SolutionA vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
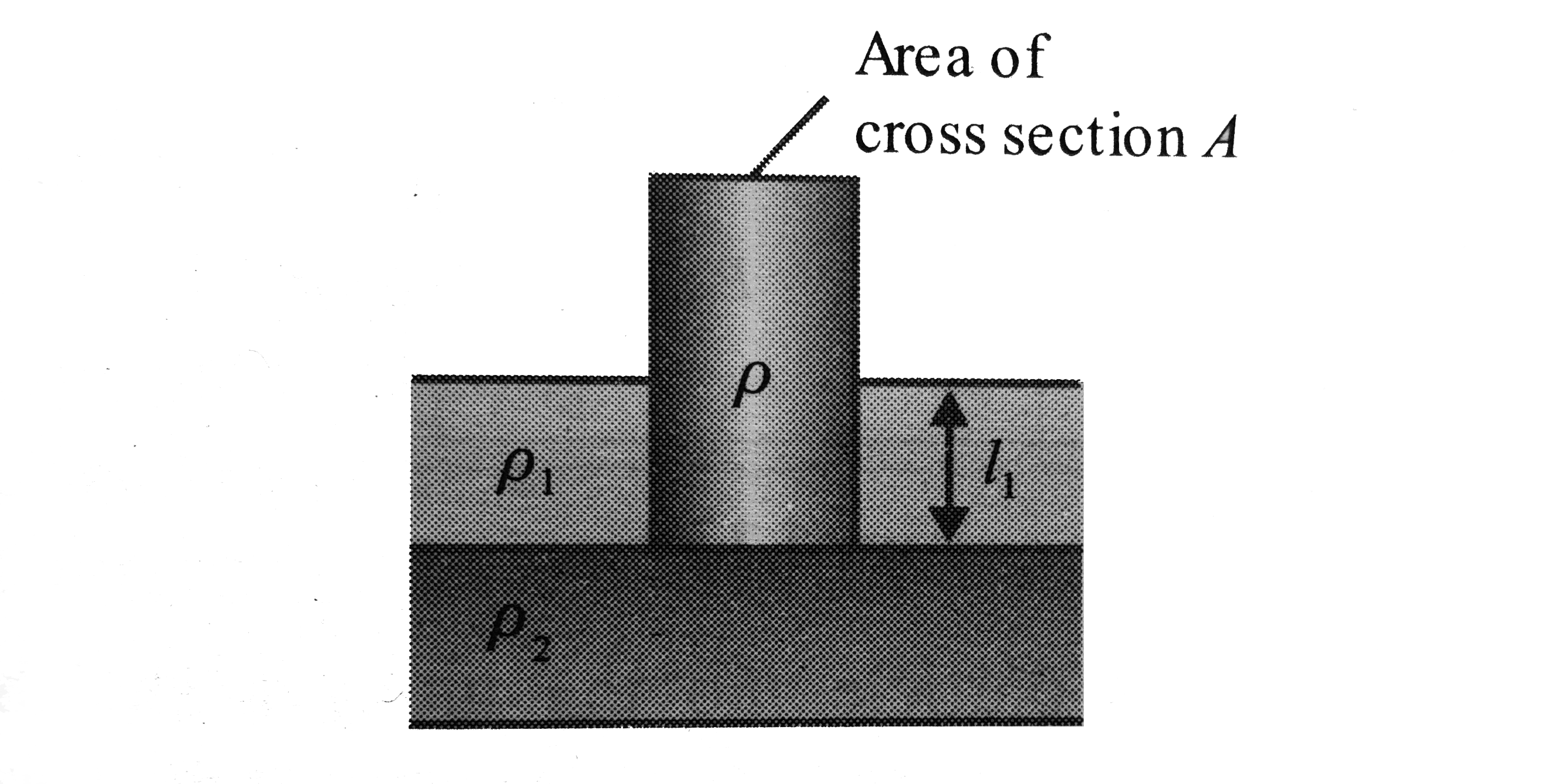
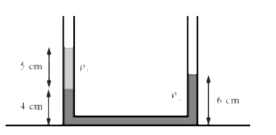
View SolutionA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
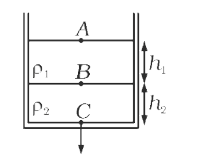
View SolutionA large tank is filled with two immiscible liquids of densities ρ1andρ2 A small hole is made at the base of the tank and liquid of density ρ2 starts flowing out of it. Three points A, B and C are marked on a vertical line. Velocity with which liquid leaves the hole is :
View SolutionTwo miscible liquids of densities 1.2gm/cm and 1.4gm/cm aer mixed with a proportion ratio of their volumes equal to 2.5: what is the density of redulting liquid?
View Solution
