Two separated air bubbles (radii 0.004mand0.002m) formed of the same liquid (surface tension 0.07N/m) come together to form a double bubble. Find the radius and the sence of curvature of the internal film surface common to both the bubbles.
Excess pressure inside first soap bubble
p1=p0+4Tr1
Excess pressure inside second soap bubble
p2=p0+4Tr2
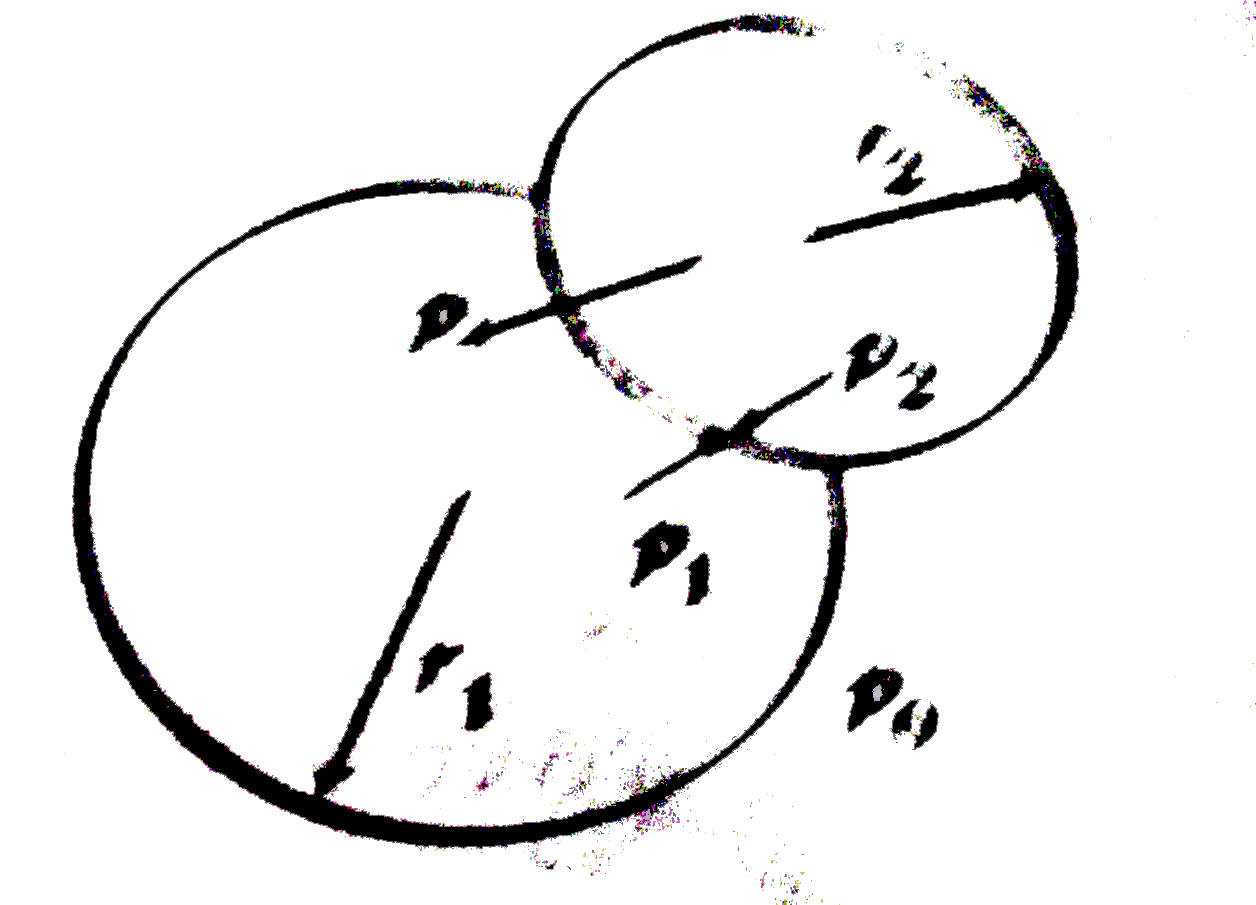
∵ r2<r1∴p2>p1
i.e., pressure inside the smaller bubble will be more. The excess pressure
p=p2−p1=4T(r1−r2r1r2)
This excess pressure acts from concave to convex side, the interface will be concave towards smaller bubble and convex towards larger bubble. Let R be the radius of interface then,
p=4TR
From Eqs. (i) and (ii),
R=r1r2r1−r2=(0.004)(0.002)(0.004−0.002)=0.004m
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Example 13.33
Explore 1 Video
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Example 13.34
Explore 1 Video
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Example 13.31
Explore 1 Video
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
Two separate air bubbles (radii 0.002cm and 0.004) formed of the same liquid (surface tension 0.07N/m) come together to form a double bubble. Find the radius and the sense of curvature of the internal film surface common to both the bubbles.
View SolutionTwo soap bubbles of radii 2 cm and 4 cm join to form a double bubble in air, then radius of. curvature of interface is
View SolutionTwo identical soap bubbles each of radius r and of the same surface tension T combine to form a new soap bubble of radius R. The two bubbles contain air at the same temperature. If the atmospheric pressure is p0 then find the surface tension T of the soap solution in terms of p0, r and R. Assume process is isothermal.
View SolutionA soap bubble A of radius 0.03 m and another bubble B of radius 0.04 m are brought together, so that the combined bubble has a common interface of radius r, then the value of r is
View SolutionTwo soap bubbles of radii 2 cm and 3 cm are brought in contact. Find the radius of curvature (in cm) of the contact surface.
View SolutionThe surface tension of a soap solution is 2×10−2N/m. To blow a bubble of radius 1cm, the work done is
View SolutionThere is an air bubble of radius 1.0 mm in a liquid of surface tension 0.075Nm−1 and density 1000kgm−3. The bubble is at a depth of 10 cm below the free surface. By what amount is the pressure inside the bubble greater than the atmospheric pressure? Take g=9.8ms−2.
View SolutionA tube of fine bore AB is connected to a manomeer M as shown. The stop cock S controls the flow in air. AB is dipped into a liquid whosw surface tension is σ. On opening the stop cock for a while, a bubble is formed at B and the manometer level is recorded, showing a difference h in the levels in the two arms. If ρ be the density of manometer liquid and r the radius of curvature of the bubble, then the surface tension σ of the liquid is given by

View SolutionTwo soap bubbles of radii a and b coalesce to form a single bubble of radius c. If the external pressure is P, find the surface tension of the soap solution.
View SolutionThere is an air bubble of radius 1.0mm in a liquid of surface tension 0.075Nm−1 and density 103kgm−3. The bubble is at a depth of 10.0cm below the free surface of a liquid. By what amount is the pressure inside the bubble greater than the atmospheric pressure?
View Solution

