Assertion If radius of cylinderical wire is doubled, then this wire can bear four times stress.
Reason By doubling the radius, area of cross-section will become four times.
If both Assertion and Reason are true and Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is false but Reason is true.
If both Assertion and Reason are false.
The correct Answer is:D
To solve the question, we need to analyze the assertion and the reason provided.
1. Understanding Stress:
Stress (σ) is defined as the force (F) applied per unit area (A) of the material. Mathematically, it is expressed as:
σ=FA
2. Area of Cross-Section of a Cylindrical Wire:
The area of cross-section (A) of a cylindrical wire is given by the formula:
A=πr2
where r is the radius of the wire.
3. Doubling the Radius:
If the radius of the cylindrical wire is doubled (i.e., r becomes 2r), we can calculate the new area of cross-section:
A′=π(2r)2=π(4r2)=4πr2=4A
This shows that the area of cross-section becomes four times the original area.
4. Effect on Stress:
Since stress is inversely proportional to the area (keeping the force constant), we can express this relationship as:
σ′=FA′=F4A=14⋅FA=σ4
This indicates that the new stress (σ') is one-fourth of the original stress (σ).
5. Conclusion:
The assertion states that if the radius of the cylindrical wire is doubled, then the wire can bear four times the stress. However, our calculations show that the stress actually decreases to one-fourth of its original value. Therefore, the assertion is false.
6. Reason Analysis:
The reason states that by doubling the radius, the area of cross-section will become four times. This is indeed true, as we calculated earlier.
Final Answer:
- The assertion is false, and the reason is true. Therefore, the correct conclusion is that the assertion does not hold true based on the reasoning provided.
Stress (σ) is defined as the force (F) applied per unit area (A) of the material. Mathematically, it is expressed as:
σ=FA
The area of cross-section (A) of a cylindrical wire is given by the formula:
A=πr2
where r is the radius of the wire.
If the radius of the cylindrical wire is doubled (i.e., r becomes 2r), we can calculate the new area of cross-section:
A′=π(2r)2=π(4r2)=4πr2=4A
This shows that the area of cross-section becomes four times the original area.
Since stress is inversely proportional to the area (keeping the force constant), we can express this relationship as:
σ′=FA′=F4A=14⋅FA=σ4
This indicates that the new stress (σ') is one-fourth of the original stress (σ).
The assertion states that if the radius of the cylindrical wire is doubled, then the wire can bear four times the stress. However, our calculations show that the stress actually decreases to one-fourth of its original value. Therefore, the assertion is false.
The reason states that by doubling the radius, the area of cross-section will become four times. This is indeed true, as we calculated earlier.
- The assertion is false, and the reason is true. Therefore, the correct conclusion is that the assertion does not hold true based on the reasoning provided.
Similar Questions
Assertion: When radius of circular loop carrying current is doubled, its magnetic moment becomes four times.
Reason: Magnetic moment depends on area of the loop.
View SolutionAssertion: When radius of circular loop carrying current is doubled, its magnetic moment becomes four times.
Rrason: Magnetic moment depends on area of the loop.
View Solution
Knowledge Check
A light rod of length 2 m is suspended from ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 0.1 cm sq. and the other of brass of cross-section 0.2 cm sq. Along the rod at what distance a weight may be hung to produce equal stresses in the wires?
(YSteel=2×1011Nm−2,YBass=1×1011Nm−2)A43m from steel wireB43m from brass wireC1 m from steel wireD14m from brass wireIf the work done in stretching a wire by 1mm is 2J, then work necessary for stretching another wire of same material but with double radius of cross -section and half of the length by 1mm is
A16JB8JC4JD14J
A force F doubles the length of wire of cross-section a The Young modulus of wire is
View SolutionIf the radius of a cylinder is doubled and the height remains same, the volume will be (a) doubled (b) halved (c) same (d) four times
View SolutionStatement 1: When radius of a circular loop carrying current is doubled, its magnetic moment becomes four times.
Statement 2: Magnetic moment depends on the area of the loop.
View SolutionWhat force is required to stretch a steel wire to double its length when its area of cross section 1 cm2 and Young.s modulus 2×1011N/m2.
View SolutionIf a wire is stretched to four times its length, then the specific resistance of the wire will
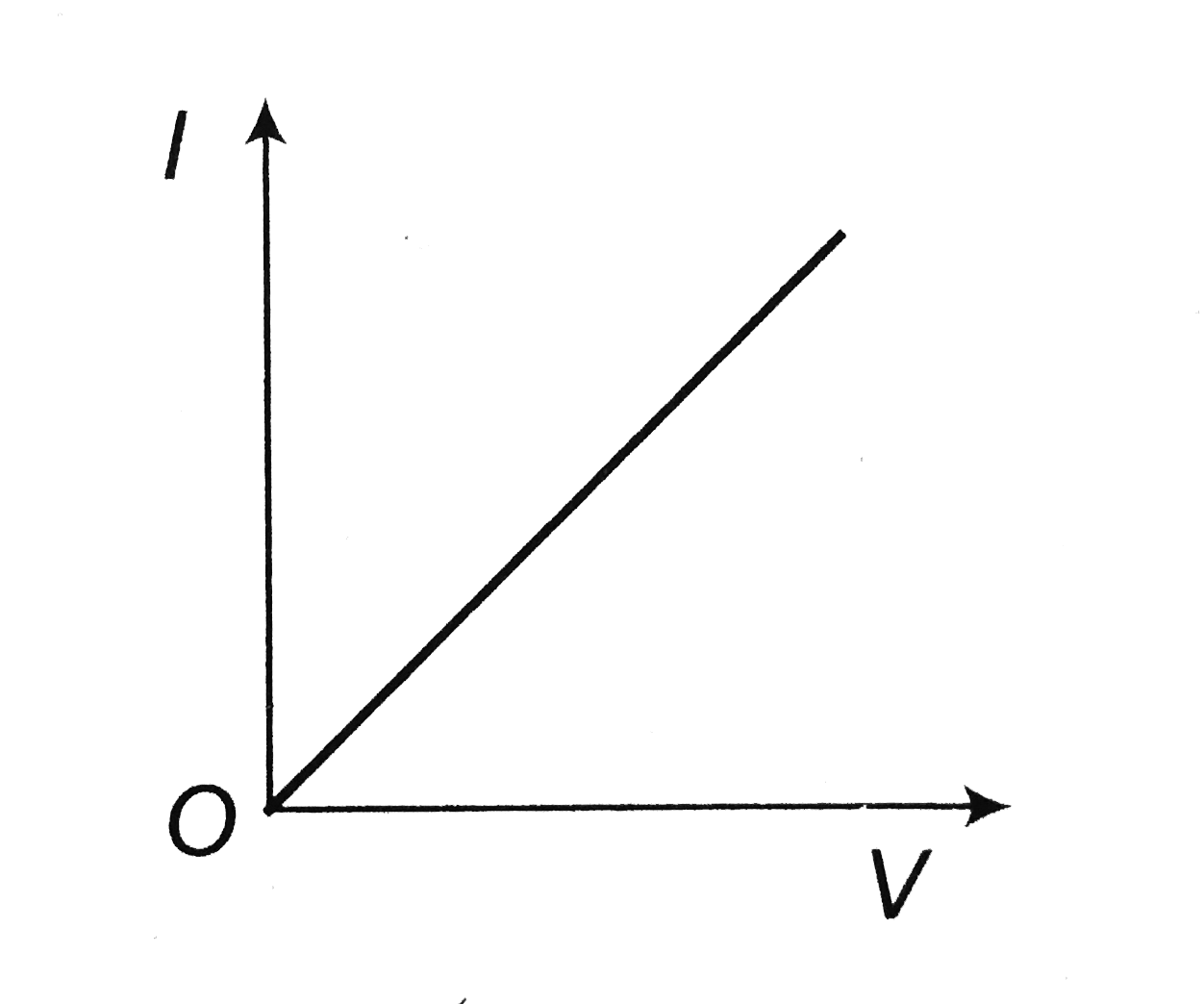
View SolutionI−V characterstic of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
View Solution
