Two springs have force constants k1 and k2(k1>k2). On which spring is more work done, if (i) they are stretched by the same force and (ii) they are stretched by the same amount ?
To solve the problem, we will analyze the work done on two springs with different force constants, k1 and k2 (where k1>k2), under two different conditions: (i) when they are stretched by the same force, and (ii) when they are stretched by the same amount.
1. Understanding the Force on the Springs:
- Let the force applied to both springs be F.
- The force exerted by a spring is given by Hooke's Law: F=k⋅x, where k is the spring constant and x is the displacement.
2. Finding Displacement for Each Spring:
- For spring 1: F=k1⋅x1 ⇒ x1=Fk1
- For spring 2: F=k2⋅x2 ⇒ x2=Fk2
3. Calculating Work Done:
- The work done on a spring is given by the formula:
W=12kx2
- For spring 1:
W1=12k1x21=12k1(Fk1)2=F22k1
- For spring 2:
W2=12k2x22=12k2(Fk2)2=F22k2
4. Comparing Work Done:
- Since k1>k2, it follows that 1k1<1k2.
- Therefore, W1<W2.
- Conclusion: More work is done on spring 2.
Part (ii): When stretched by the same amount
1. Understanding the Displacement:
- Let the displacement for both springs be x.
- Thus, for both springs, we have x1=x2=x.
2. Calculating Work Done:
- For spring 1:
W1=12k1x2
- For spring 2:
W2=12k2x2
3. Comparing Work Done:
- Since k1>k2, it follows that W1>W2.
- Conclusion: More work is done on spring 1.
Final Answers:
- (i) More work is done on spring 2.
- (ii) More work is done on spring 1.
- Let the force applied to both springs be F.
- The force exerted by a spring is given by Hooke's Law: F=k⋅x, where k is the spring constant and x is the displacement.
- For spring 1: F=k1⋅x1 ⇒ x1=Fk1
- For spring 2: F=k2⋅x2 ⇒ x2=Fk2
- The work done on a spring is given by the formula:
W=12kx2
- For spring 1:
W1=12k1x21=12k1(Fk1)2=F22k1
- For spring 2:
W2=12k2x22=12k2(Fk2)2=F22k2
- Since k1>k2, it follows that 1k1<1k2.
- Therefore, W1<W2.
- Conclusion: More work is done on spring 2.
- Let the displacement for both springs be x.
- Thus, for both springs, we have x1=x2=x.
- For spring 1:
W1=12k1x2
- For spring 2:
W2=12k2x2
- Since k1>k2, it follows that W1>W2.
- Conclusion: More work is done on spring 1.
- (i) More work is done on spring 2.
- (ii) More work is done on spring 1.
Similar Questions
Two springs have their force constant as k1 and k2(k1>k2). When they are streched by the same force.
View SolutionTwo springs have their force constant as K1 and K2(K1<K2). When they are stretched by the same force:
View SolutionSprings Aand B are identical except that A is stiffer than B. In which spring more work is done if(a) both are stretched by same amount ? (b) both are stretched by the same force ?
View SolutionTwo springs have force constants kA such that kB=2kA. The four ends of the springs are stretched by the same force. If energy stored in spring A is E, then energy stored in spring B is
View SolutionTwo springs have spring constants k1andk2(k1≠k2). Both are extended by same force. If their elastic potential energical are U1andU2, then U2 is
View SolutionTwo springs have spring constants k1andk2(k1≠k2). Both are extended by same force. If their elastic potential energical are U1andU2, then U1:U2 is
View SolutionTwo similar springs P and Q have spring constant KP and KQ such that KP>KQ. They are stretched, first by the same amount (case a), then the same force (case b). The work done by the spring WP and WQ are related as, in case (b), respectively
View SolutionTwo springs A and B (KA=2KB) are stretched by same suspended weights then ratio of workdone in stretching is -
View SolutionA spring of force constant K is cut in two parts at its one third length. When both the parts are stretched by same amount, the work done in the two parts, will be :−
View SolutionThere are two ideal springs of force constants K1 and K2 respectively. When both springs are relaxed the separation between free ends is L. Now the particle of mass m attached to free end of left spring is displaced by distance 2L towards left and then released. assuming the surface to be frictionless. (K1K2=43). (Neglect size of the block)
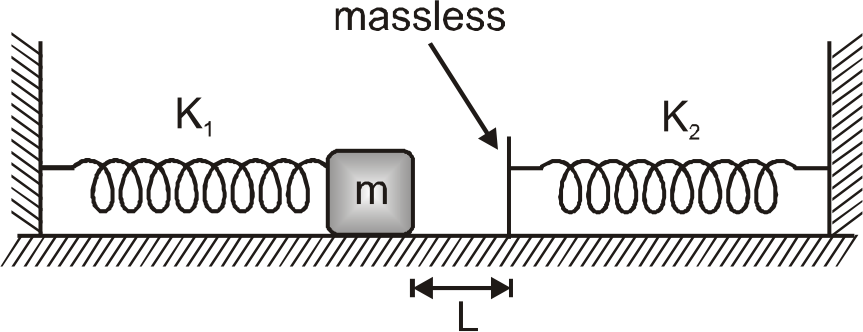
The time interval after which mass 'm' hits the right spring will be
View Solution

