A block of mass 2 kg is being brought down by a string. If the block acquires a speed 1(m)/(s) in dropping down 25 cm, find the work done by the string in the process.
To solve the problem step by step, we will follow the outlined procedure:
Step 1: Understand the Problem
We have a block of mass m=2kg that is being brought down by a string. The block drops a distance of s=25cm (which we will convert to meters) and acquires a speed of v=1m/s. We need to find the work done by the string on the block.
Step 2: Convert Units
Convert the displacement from centimeters to meters:
s=25cm=25100m=0.25m
Step 3: Use the Third Equation of Motion
We can use the third equation of motion to find the acceleration a:
v2−u2=2as
Here, the initial velocity u=0 (since it starts from rest), and substituting the known values:
12−02=2a(0.25)
1=0.5a
a=10.5=2m/s2
Step 4: Draw the Free Body Diagram
In the free body diagram, we have:
- Weight of the block acting downward: mg
- Tension in the string acting upward: T
Using Newton's second law:
mg−T=ma
Substituting the values:
2g−T=2a
Where g≈10m/s2:
2(10)−T=2(2)
20−T=4
T=20−4=16N
Step 5: Calculate Work Done by the String
The work done by the tension in the string is given by:
W=T⋅s⋅cos(θ)
Where θ is the angle between the tension and the displacement. Since the tension acts upward and the displacement is downward, θ=180∘ and cos(180∘)=−1:
W=16⋅0.25⋅(−1)
W=−4J
Final Answer
The work done by the string is −4J.
---
We have a block of mass m=2kg that is being brought down by a string. The block drops a distance of s=25cm (which we will convert to meters) and acquires a speed of v=1m/s. We need to find the work done by the string on the block.
Convert the displacement from centimeters to meters:
s=25cm=25100m=0.25m
We can use the third equation of motion to find the acceleration a:
v2−u2=2as
Here, the initial velocity u=0 (since it starts from rest), and substituting the known values:
12−02=2a(0.25)
1=0.5a
a=10.5=2m/s2
In the free body diagram, we have:
- Weight of the block acting downward: mg
- Tension in the string acting upward: T
mg−T=ma
Substituting the values:
2g−T=2a
Where g≈10m/s2:
2(10)−T=2(2)
20−T=4
T=20−4=16N
The work done by the tension in the string is given by:
W=T⋅s⋅cos(θ)
Where θ is the angle between the tension and the displacement. Since the tension acts upward and the displacement is downward, θ=180∘ and cos(180∘)=−1:
W=16⋅0.25⋅(−1)
W=−4J
The work done by the string is −4J.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:CHECK POINT 6.1
Explore 20 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:CHECK POINT 6.2
Explore 20 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:E Integer Type Questions
Explore 11 Videos
Similar Questions
A block of mass 30.0 kg is being brought down by a chain. If the block acquires as speed of 40.0cms in dropping down 2.00 m ,find the work done by the chain during the process.
View SolutionA block of mass 30.0 kg is being brought down by a chain. If the block acquires as speed of 40.0cm/s in dropping down 2.00 m ,find the work done by the chain during the process.
View SolutionA block of mass 5kg is being raised vertically upwards by the help of a string attached to it. It rises with an acceleration of 2ms−2. Find the work done by the tension in the string if the block rises by 2.5m. Also find the work done by the gravity and the net work done.
View SolutionThe block of mass m is at rest. Find the tension in the string A .

View SolutionA man pulls out a block of mass m from the depth d with help of a light string. If acceleration of the block is g2 then the work done by the string on the block will be
View SolutionA block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
View SolutionIn the shown figure, the heavu block of mass 2kg rests on the horizontal surface and the lighter block of mass 1kg is dropped from a height of 0.9m. At the instant the string gets taut, find the upwards speed (in m/s ) of the heavy block.
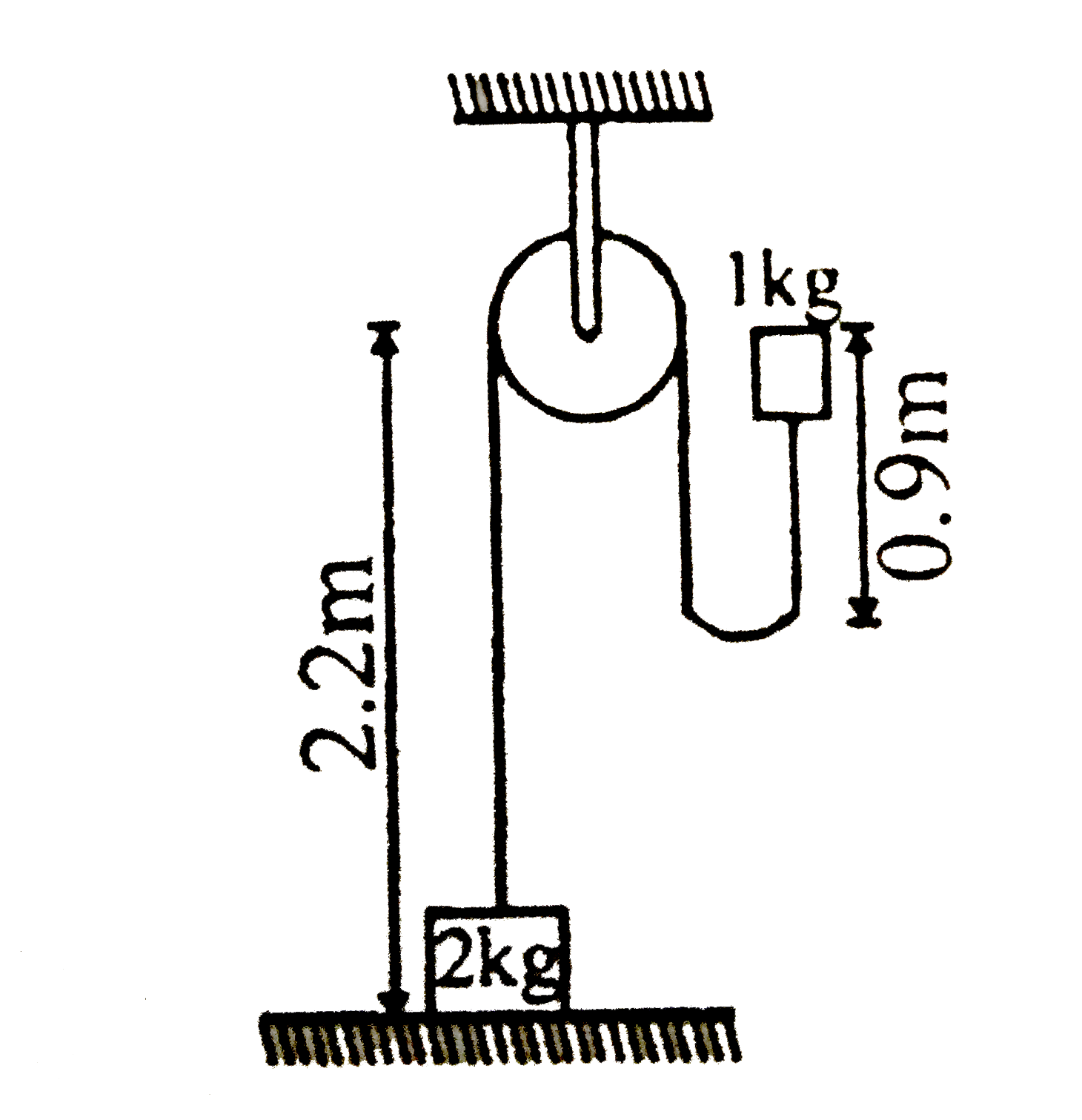
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms−2)

View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

View SolutionA small pulley of radius 20 cm and moment of inertia 0.32kg−m2 is used to hang a 2 kg mass with the help of massless string. If the block is released, for no slipping condition find the acceleration of the block ( in m/s2).
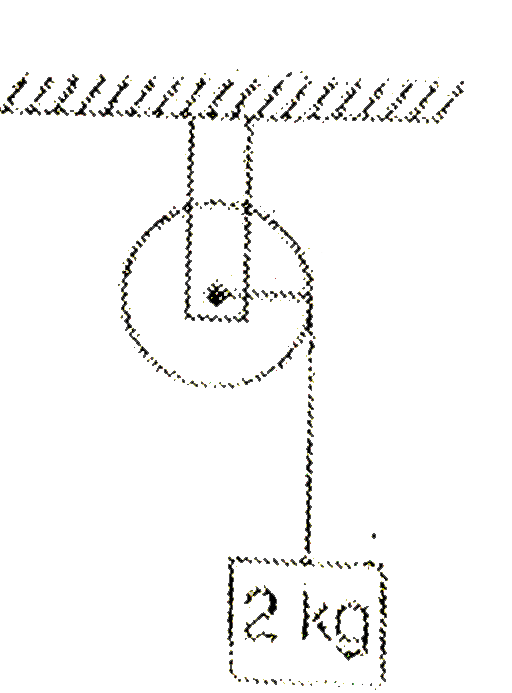
View Solution

