In the diagram shown in figure, match the following columns (take g=10ms−2)

Column IColumn II(A) Normal reaction(p) 12 SI unit(B) Force of friction(q) 20 SI unit(C) Acceleration of block(r) zero(s) 2 SI unit
The correct Answer is:A→q,B→p,C→s
N=mg−20√2sin45∘=20N
fμkN=12N
Since, 20√2cos45∘>μN block will move and kinetic friction will act,
a=20√2cos45∘−μkNm=20−124=2ms−2
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Medical entrances gallery
Explore 39 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Chapter exercises (A) Taking it together
Explore 71 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
In the diagram shown in figure, match the following (g=10m/s2)

Column-IColoumn-II(A)Acceleration of 2kg block(P)8 Si unit(B)Net force on 3kg block(Q)25 SI unit(C)Normal reaction between 2 kg and 1kg(R)2 SI unit(D)Normal reaction between 3 kg and 2kg (S) 45 SI unit(T) None
View SolutionIn the diagram shown in figure. Match the following columns.
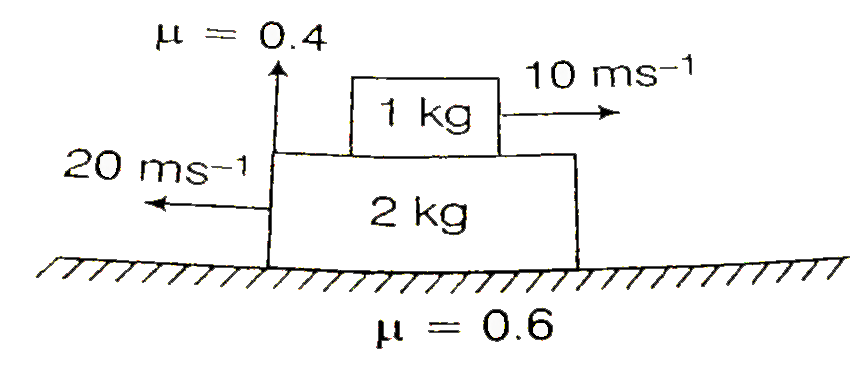
Colmun IColumn II(A) Absolute acceleration of 1 kg block(p)11ms−2(B) Absolute acceleration of 2 kg block(q)6ms−2(C) Relative acceleration between the two(r)17ms−2(s)None
View SolutionA balloon rises up with constant net acceleration of 10m/s2. After 2 s a particle drops from the balloon. After further 2 s match the following : (Takeg=10m/s2)
Column IColumn II(A)Height of perticle from ground(p)Zero(B)Speed of particle(q)10SIunits(C)Displacement of Particle(r)40SIunits(D)Acceleration of particle(s)20SIunits
View SolutionMatch the following columns.
Column IColumn II(A) Force of friction(p) Oppose motion(B) Normal reaction on a block kept on horizontal ground(q) Oppose relative motion(r) Is always mg(s) May be equal to mg(t) None
View SolutionFor the velocity -time graph shown in figure, in a time interval from t=0 to t=6s, match the following:
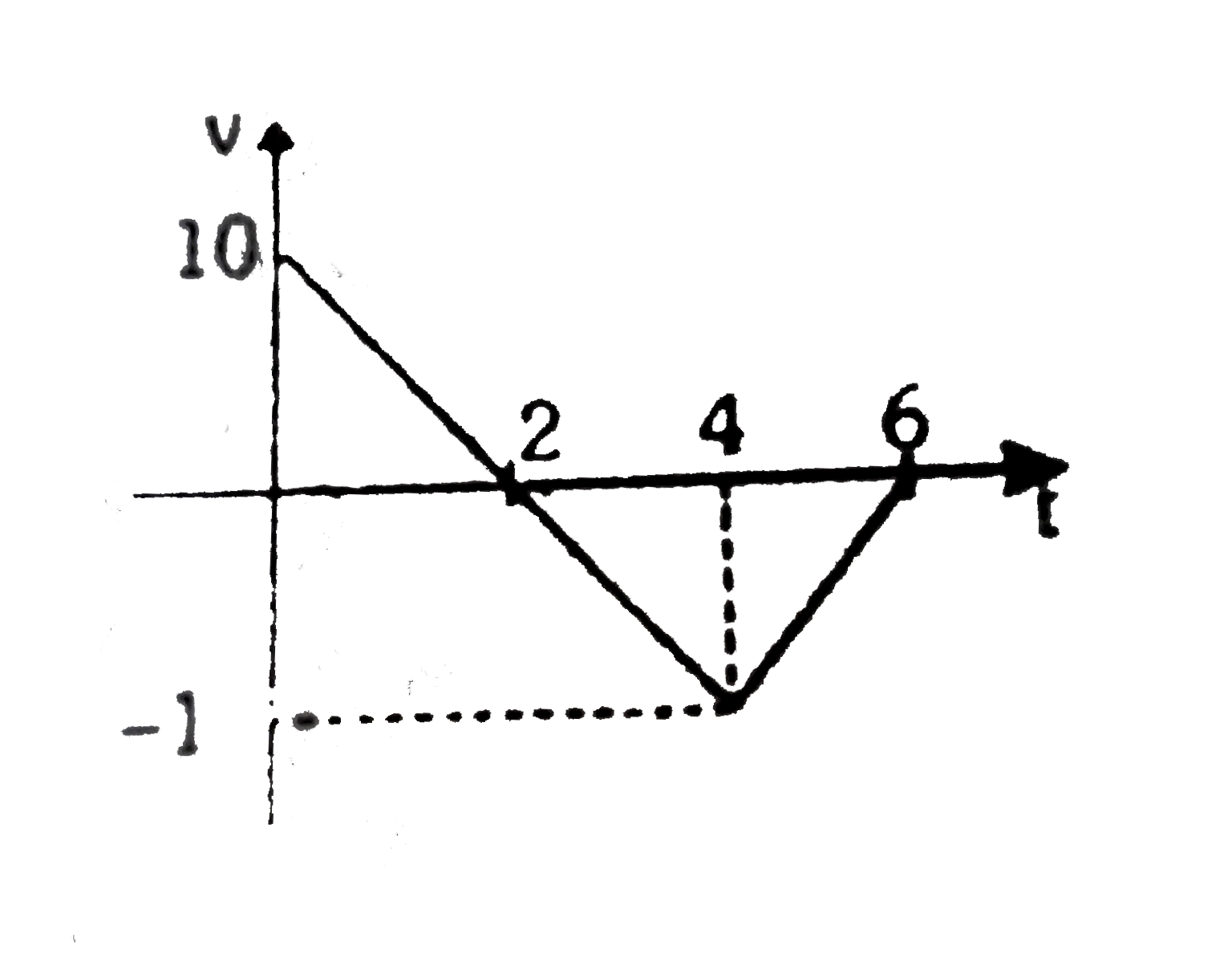
Column IColumn II(A)Change in velocity(p)−5/3SIunit(B)Average acceleration(q)−20SIunit(C)Total displacement(r)−10SIunit(D)Acceleration ay t=3s(s)−5SIunit
View SolutionA particle of mass 1 kg is projected upwards with velocity 60ms−1. Another particle of mass 2kg is just dropped from a certain height. After 2s, match the following.
[Take, g =10ms−2]
column1column2Accelertion of CMP ZeroB Velocity of CMQ 10 SI unitC Displacement of CMR 20 SI unit-S None
View SolutionIn the diagram shown in figure, all pulleys are smooth and massless and string are light. Match the following columns.

Column IColumn II(A) 1kg block(p) will remain stationary(B) 2 kg block(q) will move down(C) 3 kg block(r) will move up(D) 4 kg block(s)5ms−2(t)10ms−2
View SolutionIn the s-t equation (s=10+20t−5t2) match the following columns.
∣∣ ∣ ∣ ∣ ∣ ∣∣Column IColumn II(A)Distancec travelled in 3s(p)−20 units(B)Displacement 1 s(q)15 units(C)Initial acceleration(r)25 units(D)Velocity at 4 s(s)−10 units∣∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionIn the diamram shown in figure , match the following (g=10m/s2)
 Column IColumn II(P) Acceleration of block (in )(1) 5(Q) Acceleration of block (in )(2) 50(R) Normal reaction between and (in N)(3) 45(S) Normal reaction between and (in N)(4) 60
Column IColumn II(P) Acceleration of block (in )(1) 5(Q) Acceleration of block (in )(2) 50(R) Normal reaction between and (in N)(3) 45(S) Normal reaction between and (in N)(4) 60
View SolutionIn the arrangement shown in figure match the following
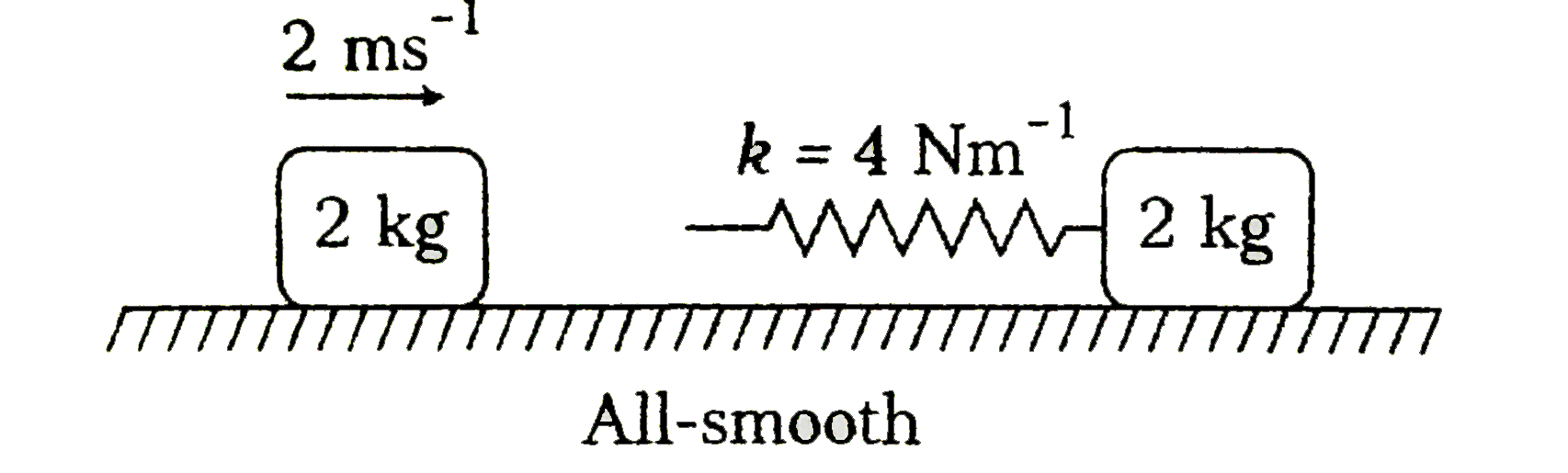
column1column2A Velocities of center of massP 2SI unitB Velocity of combined mass when compression in the spring is maximumQ 1 SI unitC Maximum compression in the springR 4 SIunitD Maximum potential energy stored in the springS 0.5SI unit
View Solution

