Block of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizontal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are
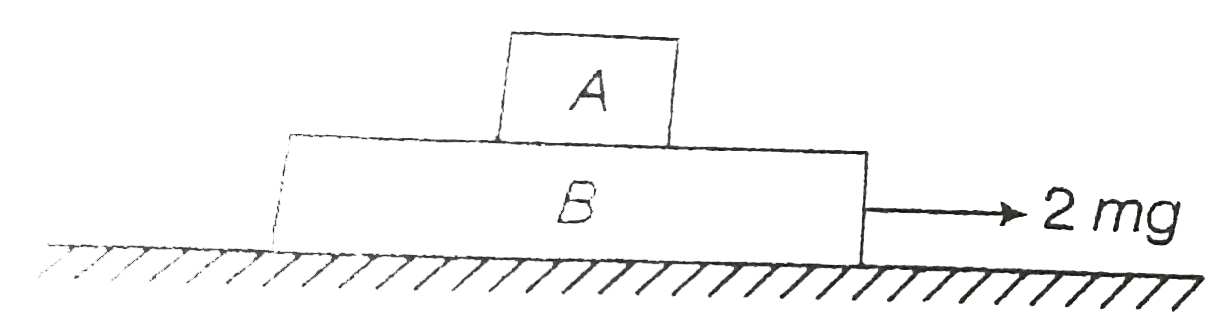
The correct Answer is:D
(d) Block A moves due to friction. Maximum value of friction can be . Therefore, maximum acceleration of A can be or . When force 2 mg is applied on lower block, common acceleration (if both move together) will be,
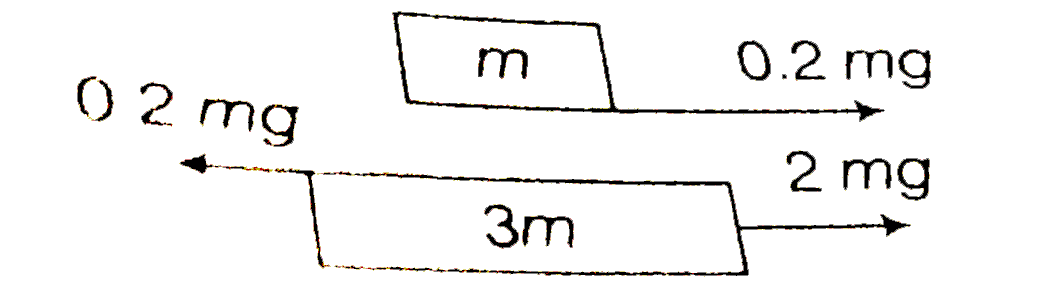
Since a =g/2 is greater than maximum acceleration of A which can be give to it by friction. Therefore slipping will take place.
(in backward direction)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Block A of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizo-ntal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are:

View SolutionA block A of mass 2kg rests on another block B of mass 8kg which rests on a horizontal floor. The coefficient of friction between A and B is 0.2 while that between B and floor is 0.5.When a horizontal floor F of 25N is applied on the block B the force of friction between A and B is
View SolutionA bolck of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
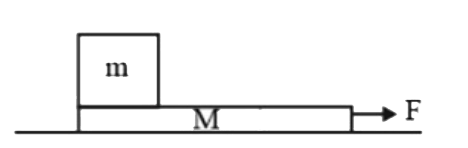
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View SolutionA block of mass m is kept over another block of mass 2 m and the system rests on a smooth horizontal surface. The coefficient of friction between the blocks is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system, when a force mg is applied to the lower block.
View SolutionA block A of mass m is placed over a plank B of mass 2m. Plank B is placed over a smooth horizontal surface. The coefficient of friction between A and B is 12 block A is given a velocity v0 towards right. Accelration of B relative to A is

View SolutionA block A of mass m is placed over a plankB of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v0 toward right Find acceleration (in ms−2 of B relative to A
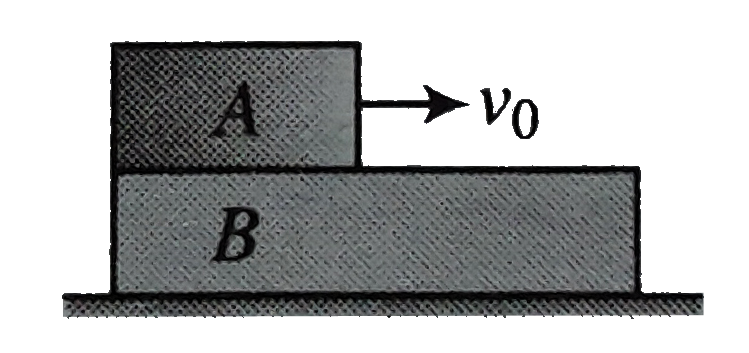
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.When a horizontal force F is applied at centre of sphere, acceleration of the plank is

View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View Solution
