An elevator and its load have a total mass of 800 kg. If the elevator, originally moving downwards at 10ms−1, is brought to rest with constant deceleration in a distance of 25 m, the tension in the supporting cable will be (g=10ms−2)
8000 N
6400 N
11200 N
9600 N
The correct Answer is:D
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given data
- Total mass of the elevator and its load, m=800kg
- Initial velocity of the elevator, u=10m/s (downward)
- Final velocity of the elevator, v=0m/s (at rest)
- Distance over which the elevator comes to rest, s=25m
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the deceleration
We can use the kinematic equation:
v2=u2+2as
Substituting the values:
0=(10)2+2a(25)
This simplifies to:
0=100+50a
Rearranging gives:
50a=−100⇒a=−2m/s2
The negative sign indicates that the acceleration is acting in the opposite direction to the motion (deceleration).
Step 3: Calculate the tension in the supporting cable
The tension T in the cable can be calculated using the formula:
T=m(g+a)
Where:
- g is the acceleration due to gravity (10 m/s²)
- a is the deceleration (which we found to be -2 m/s²)
Substituting the values:
T=800kg×(10m/s2+(−2m/s2))
This simplifies to:
T=800kg×(10−2)m/s2=800kg×8m/s2
Calculating this gives:
T=6400N
Final Answer
The tension in the supporting cable is 6400N.
---
- Total mass of the elevator and its load, m=800kg
- Initial velocity of the elevator, u=10m/s (downward)
- Final velocity of the elevator, v=0m/s (at rest)
- Distance over which the elevator comes to rest, s=25m
- Acceleration due to gravity, g=10m/s2
We can use the kinematic equation:
v2=u2+2as
Substituting the values:
0=(10)2+2a(25)
This simplifies to:
0=100+50a
Rearranging gives:
50a=−100⇒a=−2m/s2
The negative sign indicates that the acceleration is acting in the opposite direction to the motion (deceleration).
The tension T in the cable can be calculated using the formula:
T=m(g+a)
Where:
- g is the acceleration due to gravity (10 m/s²)
- a is the deceleration (which we found to be -2 m/s²)
T=800kg×(10m/s2+(−2m/s2))
This simplifies to:
T=800kg×(10−2)m/s2=800kg×8m/s2
Calculating this gives:
T=6400N
The tension in the supporting cable is 6400N.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Chapter exercises (A) Taking it together
71 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.2
15 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A 50 kg boy stands on a platform spring scale in a lift that is going down with a constant speed 3ms−1. If the lift is brought to rest by a constant deceleration in a distance of 9 m, what does the scale read during this period ? ( Take , g=9.8ms−2)
View SolutionThe total mass of an elevator with a 80 kg man in it is 1000 kg. This elevator moving upward with a speed of 8 m/sec, is brought to rest over a distance of 16m. The tension T in the cables supporting the elevator and the force exerted on the man by the elevator floor will respectively be-
View SolutionIf the elevator in shown figure is moving upwards with constant acceleration 1ms−2, tension in the string connected to block A of mass 6 kg would be ( take, g=10ms−2)
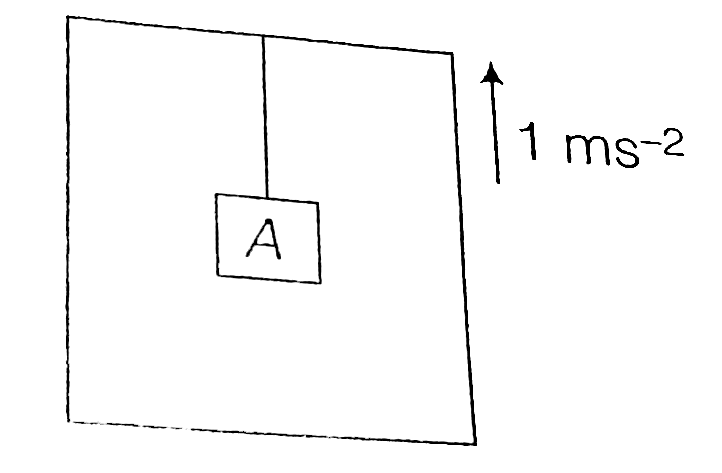
View SolutionA person of mass 60kg is inside a lift of mass 940kg and presses the button on control panel. The lift starts moving upword with an acceleration 1.0m/s2 . If g=10m/s2 , the tension in the supporting cable is.
View SolutionA stone of mass 1 kg tied at the end of a string of length 1 m and is whirled in a verticle circle at a constant speed of 3ms−1. The tension in the string will be 19 N when the stone is (g=10ms−1)
View SolutionA wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
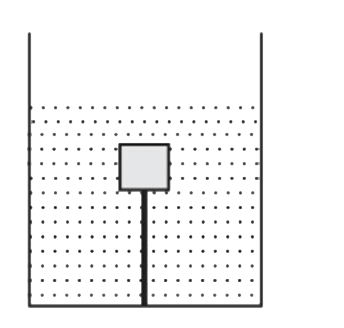
View SolutionAn elevator weighing 6000 kg is pulled upward by a cable with an acceleration of 5ms−2 . Taking g to be 10ms−2 , then the tension in the cable is
View SolutionAn elevator with passengers has a total mass of 800kg and moves slowly a vertical distance of 20.0m in 10.0s. What is the average power expended in lifting this mass ?
View SolutionYou are designing an elevator for a hospital. The force exerted on a passenger by the floor of the elevator is not to exceed 1.60 times the passenger's weight. The elevator accelerates upwards with constant accelerates upwards with constant acceleration for a distance of 3.0 m and then starts to slow down. What is the maximum speed (in ms−1) of the elevator?
View SolutionYou are designing an elevator for a hospital. The force exerted on a passenger by the floor of the elevator is not to exceed 1.60 times the passenger's weight. The elevator accelerates upwards with constant accelerates upwards with constant acceleration for a distance of 3.0 m and then starts to slow down. What is the maximum speed (in ms−1) of the elevator?
View Solution
