A rod AB rests with the end A on rough horizontal ground and the end B against a smooth vertical wall. The rod is uniform and of weight w. If the rod is in equilibrium in the position shown in figure.Find
(a)frictional force shown at A
(b) normal reaction at A
(c) normal reaction at B.

Let length of the rod is 2l. Using the three conditions of equilibrium. Anti- clockwise moment is taken as positive.
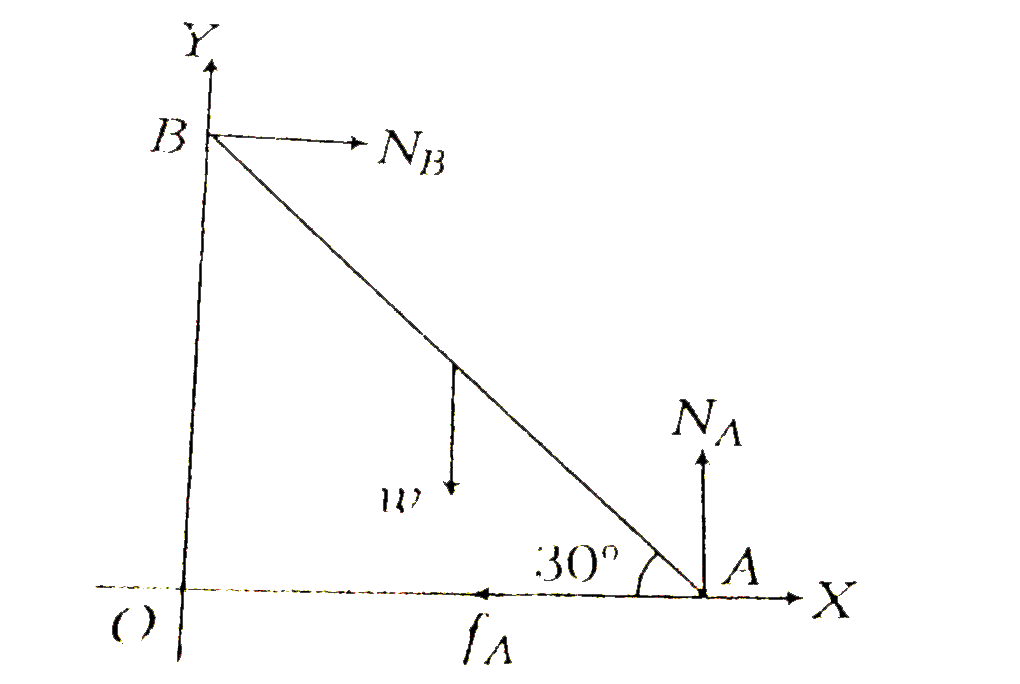
(i) ∑Fx=0
∴NB−fA=0
or NB=fA……….(i)
(ii)∑Fy=0
∴NA−w=0
or NA=w........(ii)
(iii) ∑τ0=0
∴NA(2lcos30∘)−NB(2lsin30∘)−w(lcos30∘)=0
or √3NA−NB−√32w=0........(iii)
Solving these three equations, we get
(a)fA=√32w (b) NA)=w
(c ) NB=√32w
Similar Questions
A rod AB rests with the end A on rough horizontal ground and the end B against a smooth vertical wall. The rod is uniform and of weight w. If the rod is in equilibrium in the position shown in figure.Find
(a)frictional shown at A
(b) normal reaction at A
(c) normal reaction at B.

View SolutionA uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of 530 with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
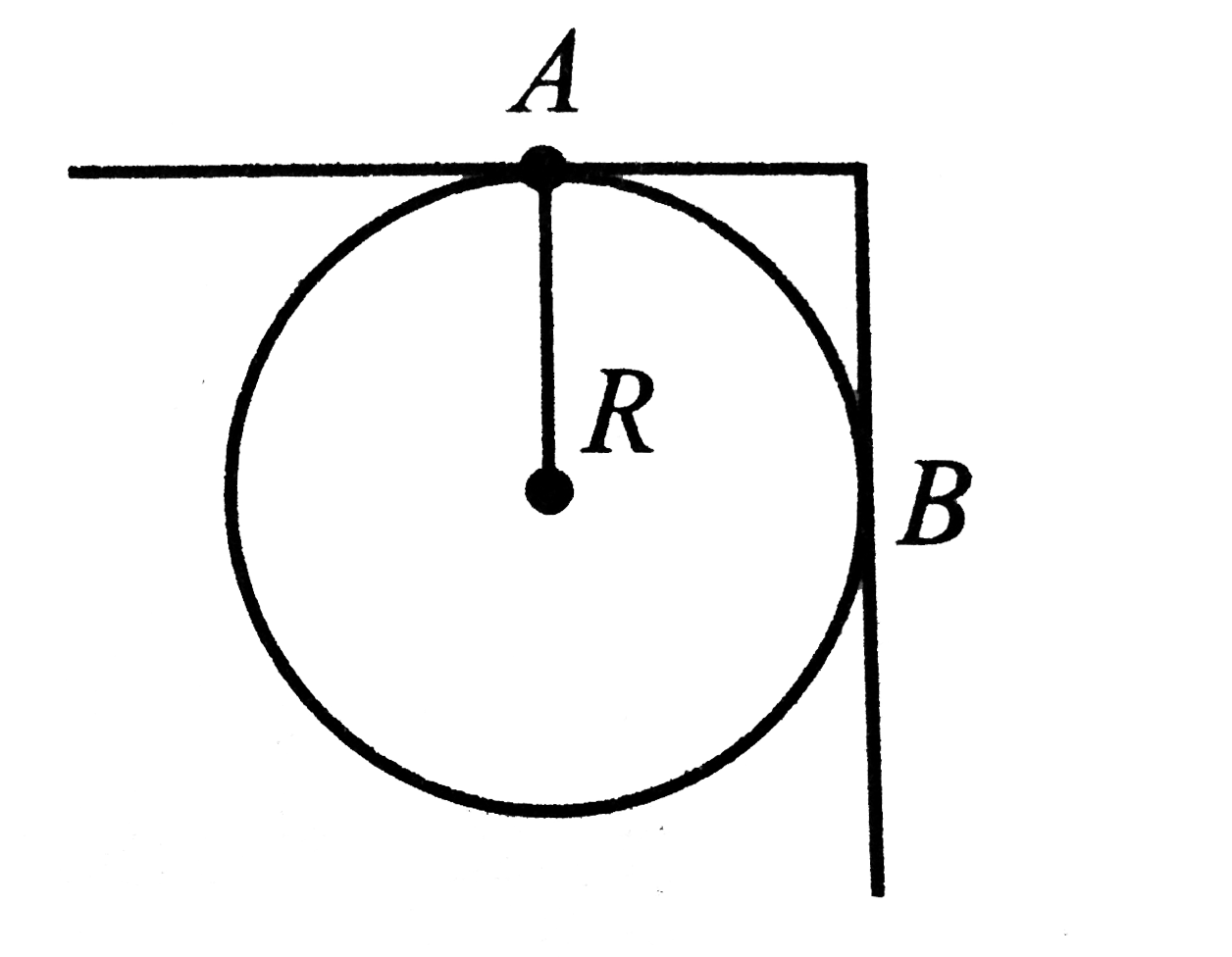
View SolutionA rod bent at right angle along its centre line is placed on a rough horizontal fixed cylinder of radius R as shown in the figure. Mass of the rod is 2m and the rod is in equilibrimu. Assume that the friction force on rod at A and B is equal in magnitude.
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
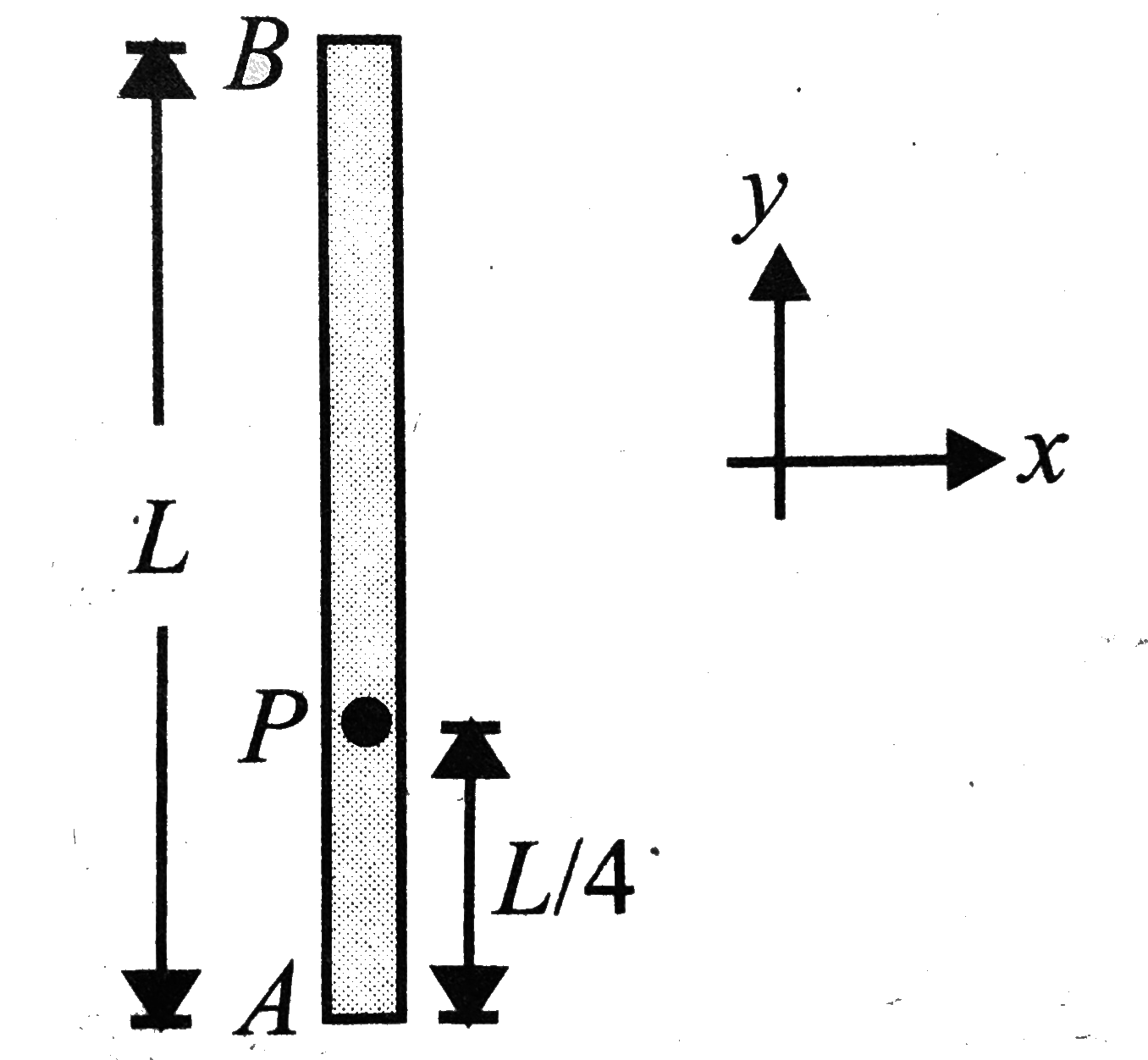
The acceleration of end B of the rod is
View SolutionA rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Normal reaction by ground on the rod

View SolutionA thin, uniform rod with negligible mass and length 0.200m is attached to the floor by a frictionless hinge at point P (as shown in fig) A horizontal spring with force constant k=4.80Nm−1 connects the other end of the rod to a vertical wall. The rod to a vertical wall. The rod is in a uniform magnetic field B=0.340T directed into the plane of the figure. There is current I=6.50 A in the rod, in the direction shown.
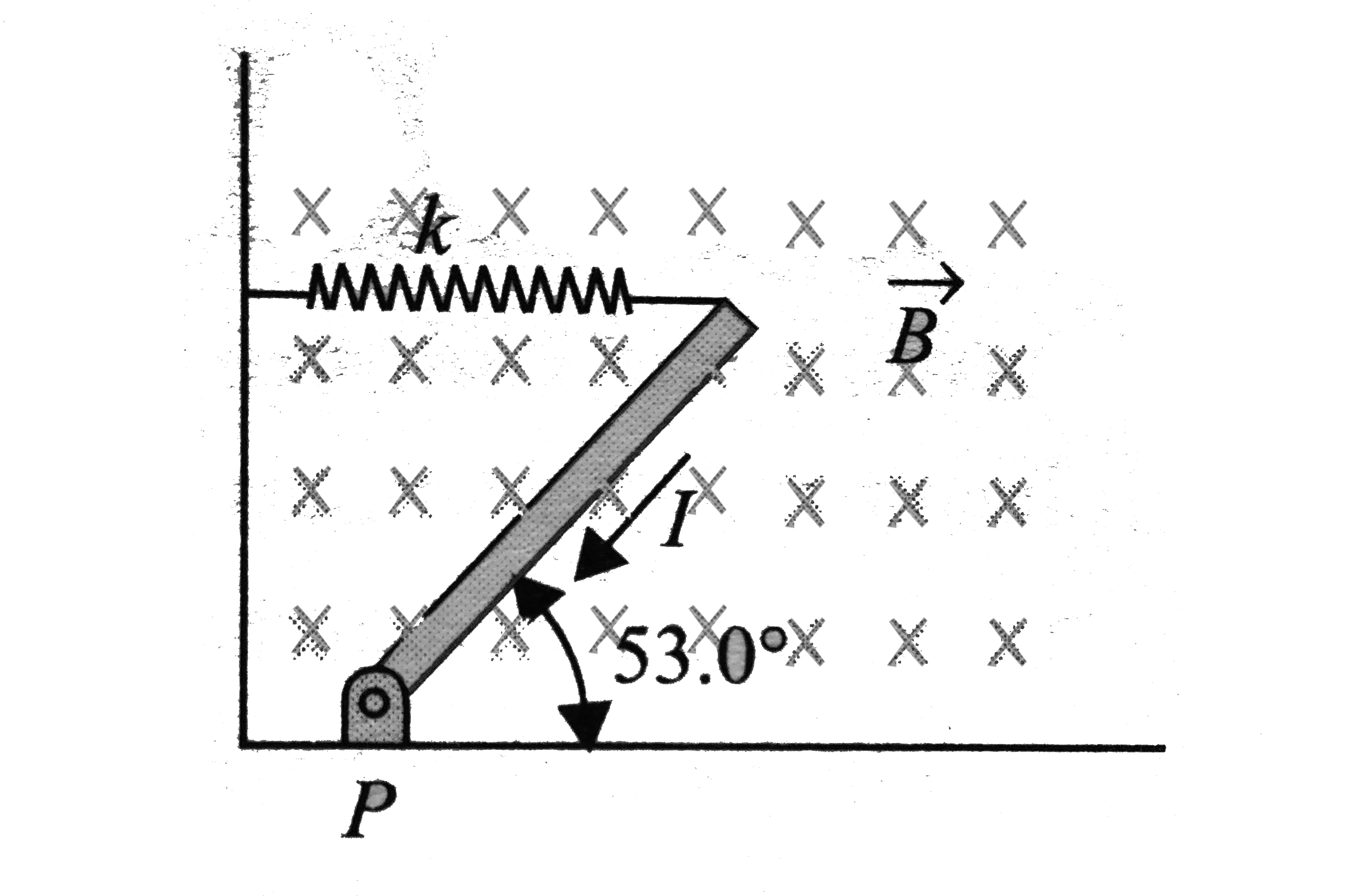
Calculate the torque due to the magnetic force on the rod, for an axis at P.
View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass m of the rod.
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:

View SolutionA uniform rod is resting freely over a smooth horizontal plane. A particle moving horizontally strikes at one end of the rod normally and gets stuck. Then
View Solution
