In the adjoining figure, the coefficient of friction between wedge (of mass M) and block (of mass m) is μ.
Find the minimum horizontal force F required to keep the block stationary with respect to wedge.

Such problems can be solved with or without using the concepte of pseudo force. Let us, solve the problem by both the methods.
a= Acceleration of ( wedge+ block ) in horizontal direction =FM+m.
(i) Inertial frame of reference ( ground) FBD of block with respect to ground ( only real forces have to be applied) with respect to ground block is moving with an acceleration a.
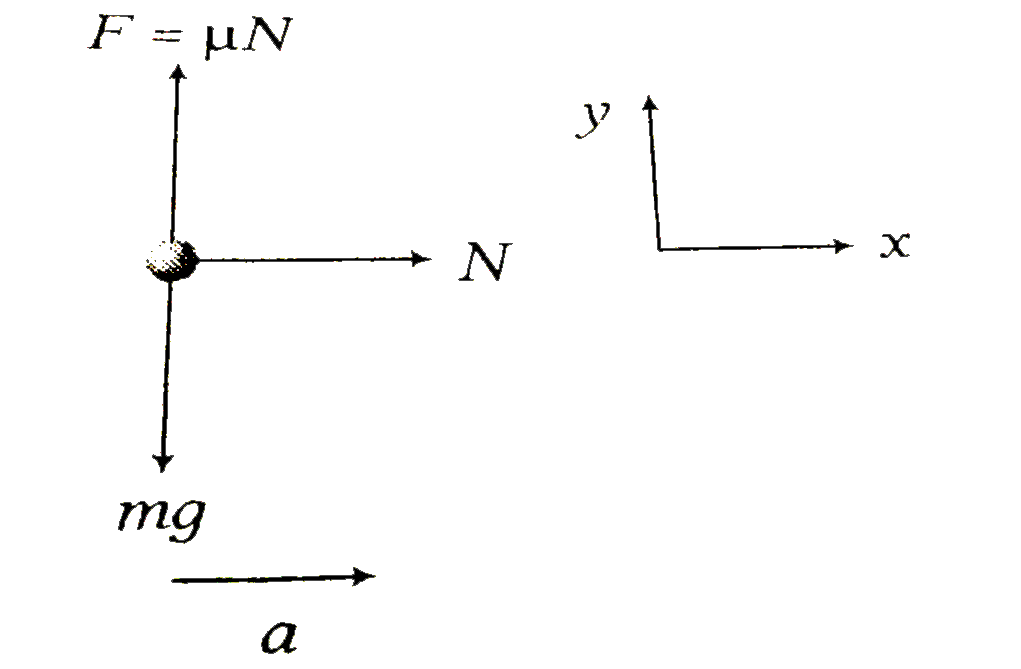
Therefore,
∑Fy=0 and ∑Fx=ma
mg=μN and N=ma
∴a=gμ
∴F=(M+m)a=(M+m)gμ
(ii) Non- inertial frame of reference ( wedge ) FBD of m with respect to wedge ( real + one pseudo force ) with respect to wedge block is stationary.

∴∑Fx=0=∑Fy
∴mg=μN
and N= ma
∴a=gμ and F=(M+m)a=(M+m)gμ
From the above discussion, we can see that from both the methods results are same.
Similar Questions
A bar of mass m is placed on a triangular block of mass M as shown in figure The friction coefficient between the two surface is μ and ground is smooth find the minimum and maximum horizontal force F required to be applied on block so that the bar will not slip on the inclined surface of block

View SolutionA block of mass m is placed over the wedge as shown in figue Coefficent of frition μ is half the minimum value required to keep it in this postion.

what is the minimum value of accleration of wedge to keep the blok statinary with respect to the wedge in either of the four cases?

View Solution
Knowledge Check
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 A0.15mgB0.05mgC0.1mgD0.45mg
A0.15mgB0.05mgC0.1mgD0.45mg
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View Solution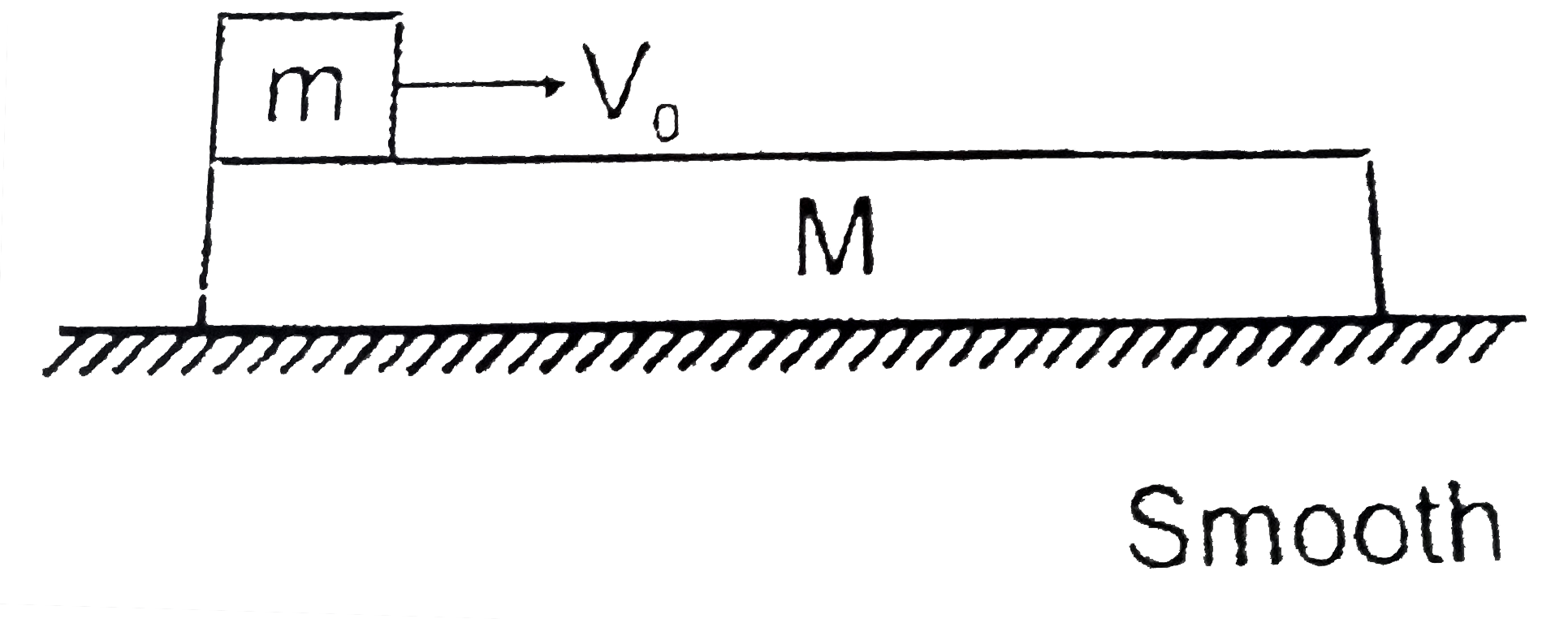
The block of mass m is kept on plank of mass M. The block is given velocity V0 as shown. The coefficient of friction between the block of mass m and plank of mass M is μ and its value is such that block becomes stationary with respect to plank before it reaches the other end. Then:
View SolutionA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionA block A of mass m which is placed a rough inclined face of a wedge of same mass being pulled through light string and with force F as shown in figure The coefficient of friction between inclined face and block A is μ while there is no friction between the ground and wedge it the whole system moves with same acceleration then find the value of F

View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View SolutionTwo blocks of masses'm' and 'M' are arranged as shown in the figure. The coefficient of friction between the two blocks is ' μ ', where as between the lower block and the horizontal surface is zero. Find the force 'F' to be applied on the upper block, for the system to be under equilibrium ?

View Solution

