Fig. shows an estimated force-time graph for a base ball struck by a bat. From this curve, determine
(i) impulse delivered to the ball
(ii) force exerted on the ball
(iii) the maximum force on the ball.
To solve the problem step by step, we will analyze the force-time graph of a baseball struck by a bat and determine the required quantities: impulse delivered to the ball, force exerted on the ball, and the maximum force on the ball.
Step 1: Determine the Impulse Delivered to the Ball
Impulse is defined as the area under the force-time graph. In this case, the graph forms a triangle.
1. Identify the base and height of the triangle:
- The base of the triangle is the time interval during which the force is applied. From the graph, this is from t=1 second to t=2.5 seconds, which gives us:
Base=2.5−1=1.5 seconds
- The height of the triangle is the maximum force exerted, which from the graph is 18000 Newtons.
2. Calculate the area of the triangle:
Area=12×Base×Height=12×1.5×18000
Area=12×1.5×18000=13500 Newton-seconds
Impulse delivered to the ball: 13500Ns
Step 2: Determine the Force Exerted on the Ball
To find the average force exerted on the ball, we can use the impulse-momentum theorem, which states that impulse is equal to the change in momentum.
1. Use the formula for force:
Impulse=Force×Δt⟹Force=ImpulseΔt
where Δt=1.5 seconds (the time interval we calculated earlier).
2. Substitute the values:
Force=135001.5=9000 Newtons
Force exerted on the ball: 9000N
Step 3: Determine the Maximum Force on the Ball
From the graph, the maximum force is simply the highest point reached on the force-time graph.
1. Identify the maximum force:
- From the graph, the maximum force is 18000 Newtons.
Maximum force on the ball: 18000N
Summary of Results
- (i) Impulse delivered to the ball: 13500Ns
- (ii) Force exerted on the ball: 9000N
- (iii) Maximum force on the ball: 18000N
- The base of the triangle is the time interval during which the force is applied. From the graph, this is from t=1 second to t=2.5 seconds, which gives us:
Base=2.5−1=1.5 seconds
- The height of the triangle is the maximum force exerted, which from the graph is 18000 Newtons.
Area=12×Base×Height=12×1.5×18000
Area=12×1.5×18000=13500 Newton-seconds
Impulse=Force×Δt⟹Force=ImpulseΔt
where Δt=1.5 seconds (the time interval we calculated earlier).
Force=135001.5=9000 Newtons
- From the graph, the maximum force is 18000 Newtons.
- (i) Impulse delivered to the ball: 13500Ns
- (ii) Force exerted on the ball: 9000N
- (iii) Maximum force on the ball: 18000N
Similar Questions
A batsman hits a cricket ball which then rolls on a level ground. After covering a short distance, the ball comes to rest. The ball slows to a stop because (a) the batsman did not hit the ball hard enough, (b) velocity is proportional to the force exerted on the ball, (c ) there is a force on the ball opposing the motion ,(d) there is no unbalanced forcr on the ball, so the ball would want to come to rest.
View SolutionA boy holds a rubber ball in his hand. The reaction force of gravity on the ball is the force exerted by the
View SolutionThe velocity time graph of a ball of mass 20g moving along a straight line on a long table is given in (figure) How much force does the table exert on the ball to bring it to rest?
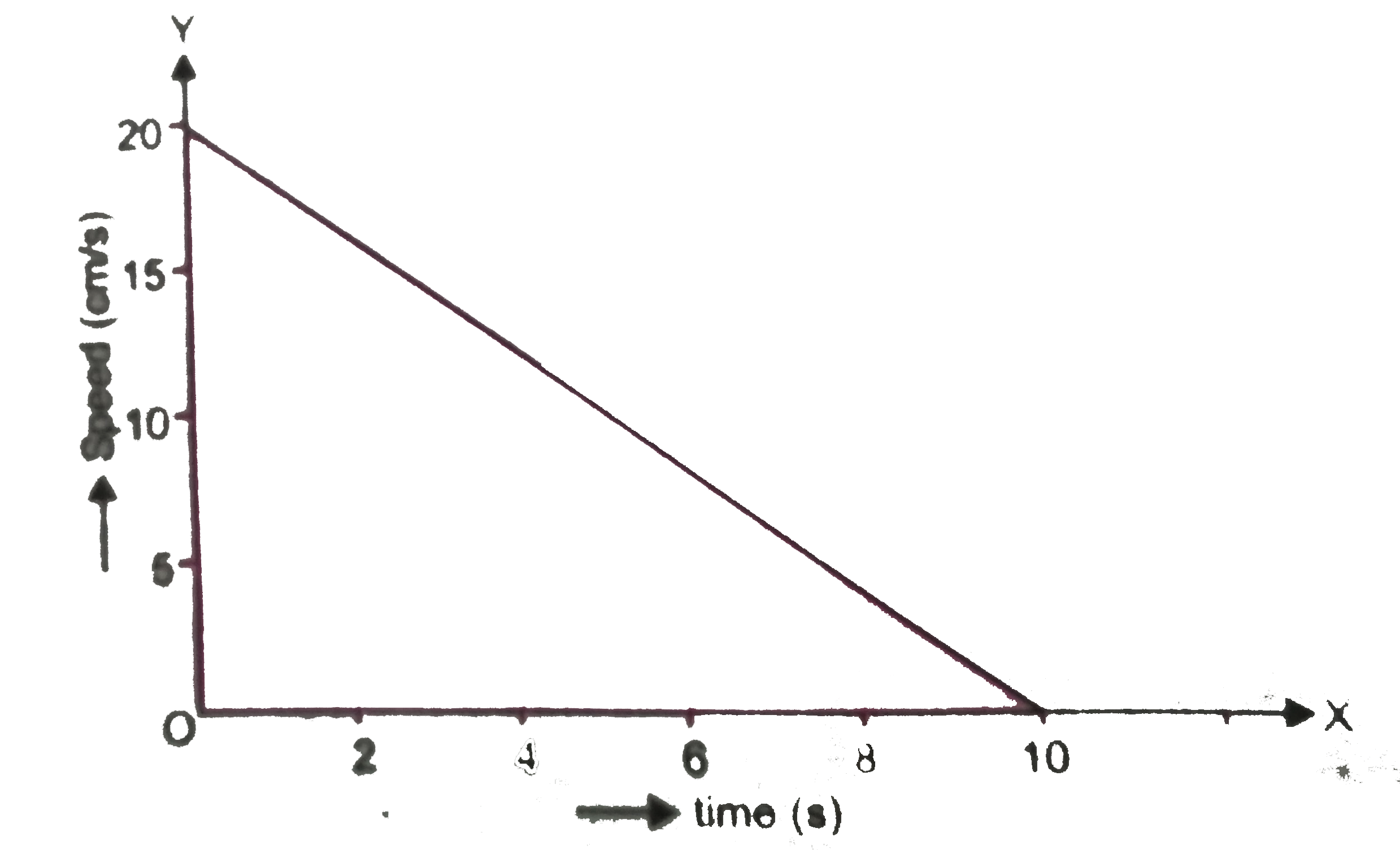 View Solution
View SolutionA cricket ball of mass 150 kg is moving with a velocity of 12m/s and is hit by a bat so that ball is turned back with a velocity of 20m/s . The force of the blow acts for 0.01 s on the ball . Find the average force exerted by the bat on the ball.
View SolutionA ball is thrown upward with an ini tial velocity of 100ms−1. After how much time will it return ? Draw velocity - time graph for the ball and find from the graph (i) the maximum height attained by the ball and (ii) height of the ball after 15 s. Take g=10ms−2 .
View SolutionA bag contains 10 red 5 blue and 7 green balls. A ball is drawn at random. Find the probability of this ball being a
(i) red ball (ii) green ball (iii) not a blue ballView SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
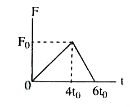
Maximum force exerted by the bat on the ball isView SolutionThe following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass 250g is thrown with a speed of 30m/s. The ball strikes a bat and it is hit straight back along the same line at a speed of 50m/s. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
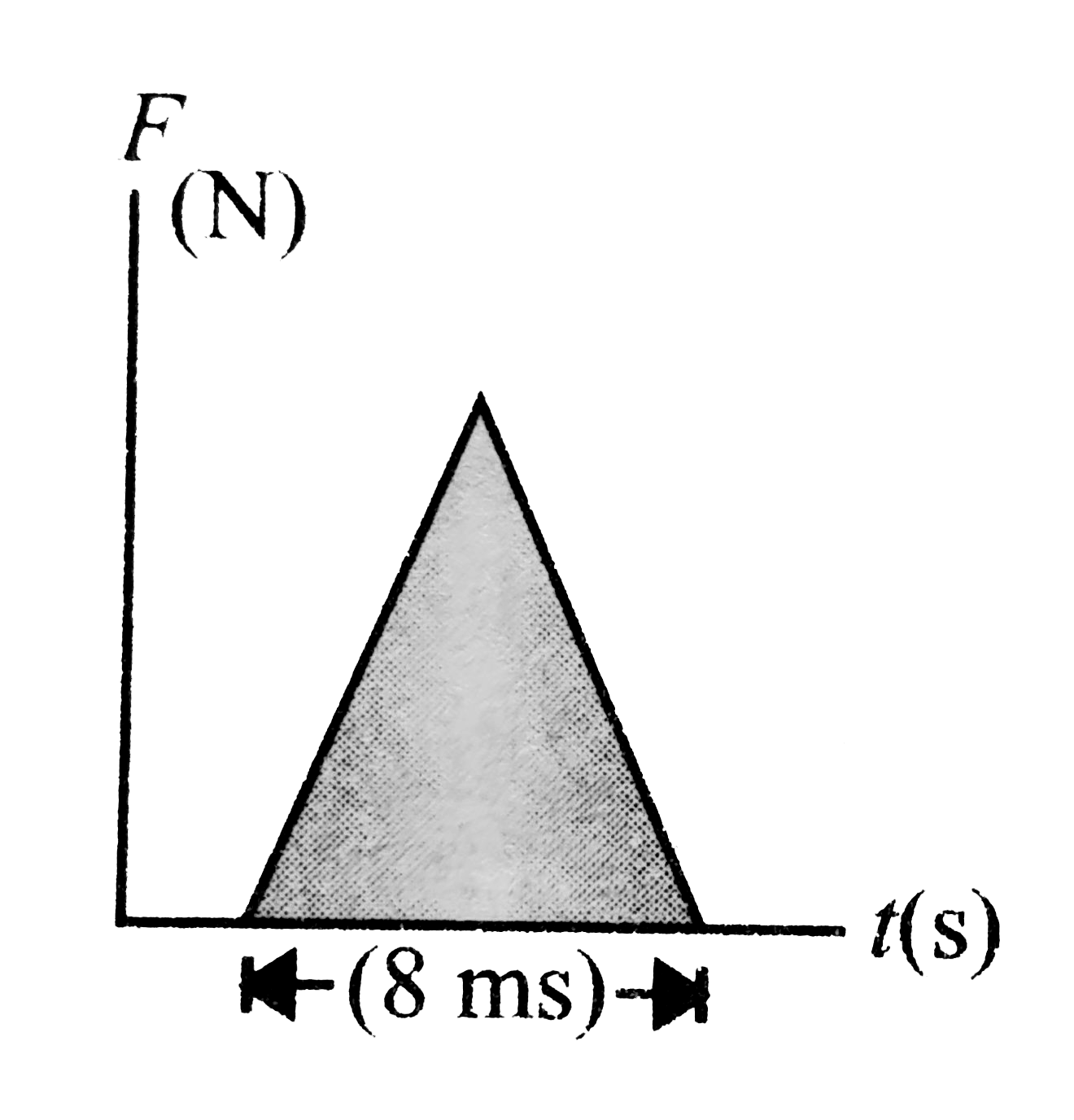
Maximum force exerted by the bat on the ball isView SolutionA ball is hanging by string from the ceiling of the roof. Draw a neat labelled diagram showing the forces acting on the ball and the string.
View SolutionVelocity versus time graph of a ball of mass 50g rolling on a concrete floor shown in (figure) Calcualte the acceleration and frictional force of the floor on the ball.
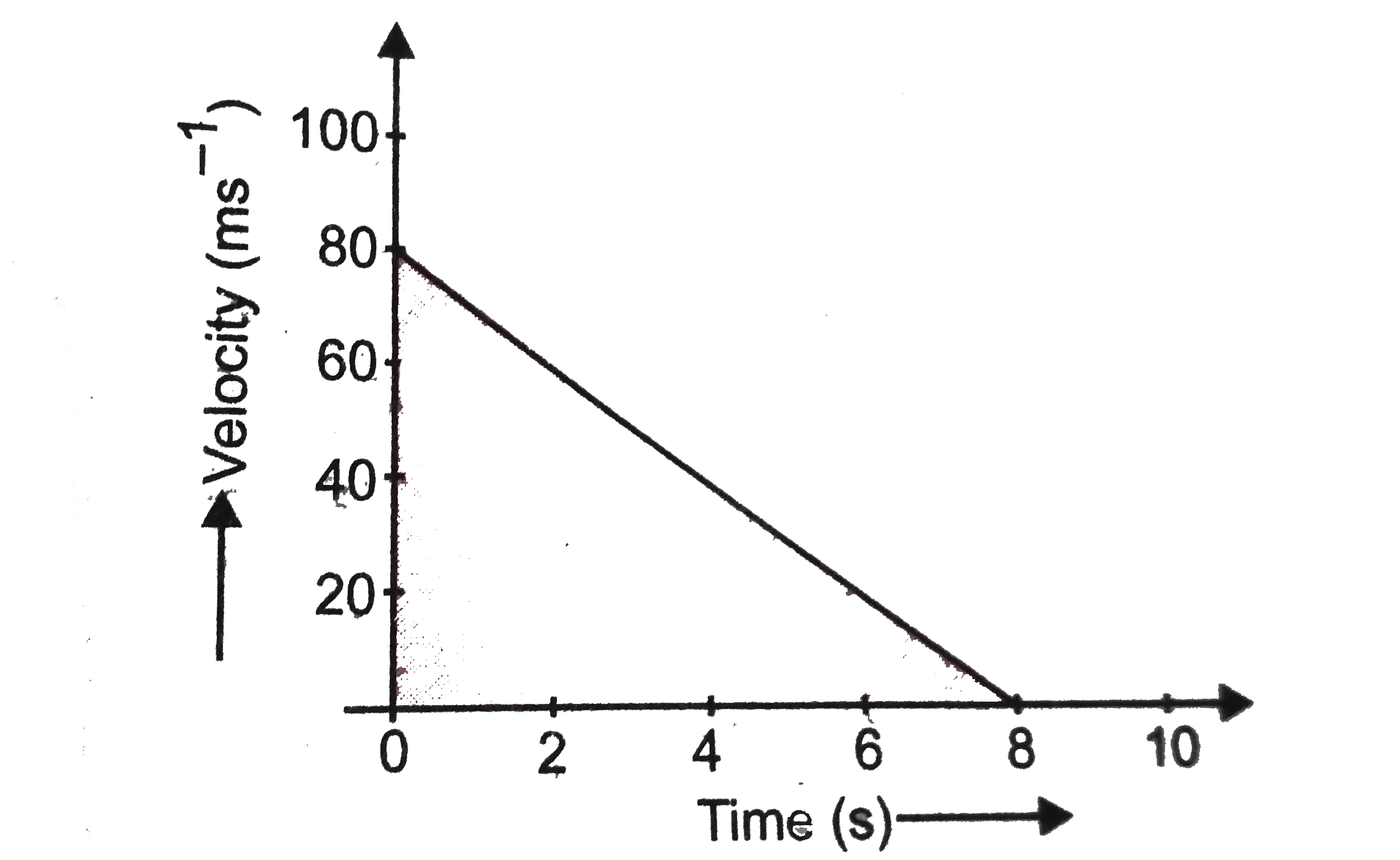 View Solution
View Solution
