A vector has a magnitude x . If it is rotated by an angle θ then magnitude of change in vector is nx. Match the following two columns.
Column I Column II(A)θ=60∘(P)n=√3(B)θ=90∘(Q)n=1(C)θ=120∘(r)n=√2(D)θ=180∘(s)n=2
The correct Answer is:A→q, B→r , C→ p, D→s
To solve the problem, we need to determine the change in magnitude of a vector when it is rotated by a given angle θ. The change in magnitude is given as n⋅x, where x is the original magnitude of the vector.
1. Understanding the Change in Vector Magnitude:
The change in magnitude of the vector when rotated by an angle θ can be expressed using the formula:
Δr=√r21+r22−2r1r2cos(θ)
where r1=x and r2=x (since both vectors have the same magnitude).
2. Simplifying the Expression:
Substituting r1 and r2 into the equation:
Δr=√x2+x2−2x2cos(θ)=√2x2(1−cos(θ))
This simplifies to:
Δr=x√2(1−cos(θ))
3. Using the Sine Double Angle Identity:
We can use the identity 1−cos(θ)=2sin2(θ/2):
Δr=x√2⋅2sin2(θ/2)=2xsin(θ/2)
4. Finding n:
We know that Δr=n⋅x, thus:
n=Δrx=2sin(θ/2)
5. Calculating n for Different Angles:
Now we will calculate n for each angle given in the options:
- For θ=60∘:
n=2sin(30∘)=2⋅12=1(matches with Q)
- For θ=90∘:
n=2sin(45∘)=2⋅1√2=√2(matches with R)
- For θ=120∘:
n=2sin(60∘)=2⋅√32=√3(matches with P)
- For θ=180∘:
n=2sin(90∘)=2⋅1=2(matches with S)
Final Matching:
- A (60°) matches with Q (n = 1)
- B (90°) matches with R (n = √2)
- C (120°) matches with P (n = √3)
- D (180°) matches with S (n = 2)
Summary of Matches:
- A - Q
- B - R
- C - P
- D - S
The change in magnitude of the vector when rotated by an angle θ can be expressed using the formula:
Δr=√r21+r22−2r1r2cos(θ)
where r1=x and r2=x (since both vectors have the same magnitude).
Substituting r1 and r2 into the equation:
Δr=√x2+x2−2x2cos(θ)=√2x2(1−cos(θ))
This simplifies to:
Δr=x√2(1−cos(θ))
We can use the identity 1−cos(θ)=2sin2(θ/2):
Δr=x√2⋅2sin2(θ/2)=2xsin(θ/2)
We know that Δr=n⋅x, thus:
n=Δrx=2sin(θ/2)
Now we will calculate n for each angle given in the options:
n=2sin(30∘)=2⋅12=1(matches with Q)
n=2sin(45∘)=2⋅1√2=√2(matches with R)
n=2sin(60∘)=2⋅√32=√3(matches with P)
n=2sin(90∘)=2⋅1=2(matches with S)
- A (60°) matches with Q (n = 1)
- B (90°) matches with R (n = √2)
- C (120°) matches with P (n = √3)
- D (180°) matches with S (n = 2)
- A - Q
- B - R
- C - P
- D - S
Topper's Solved these Questions
Similar Questions
A disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
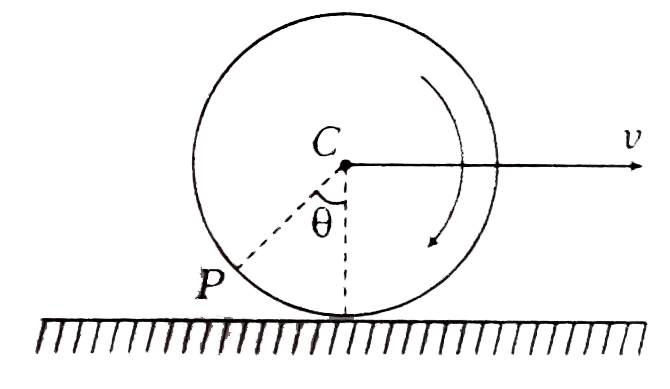
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3v
View SolutionIf θ is the abgle between two vectors A and B , then match the following two columns.
Column I Column II(A)A.B=|A×B|(P)θ=90∘(B)A.B=B2(Q)θ=0∘or180∘(C)|A+B|=|A−C|(r)A=B(D)|A×B|=AB(s)None
View SolutionTwo vector A and B have rqual magnitude x .Angle between tjem is 60∘ Then match the following two columns.
Column I Column II(A)|A+B|(P)√32x2(B)|A−B|(Q)x(C)A.B(r)√3x(D)|A×B|(s)None
View SolutionMatch the following the compounds of column I with column II.
Column-IColumn-II(A)CnH2n+2(p)Alkynes(B)CnH2n(q)Alkenes(C)CnH2n−2(r)Cyclohexane(D)C6H12(s)Paraffins or alkanes
View SolutionIf Sn=cosnθ+sinnθ then find the value of 3S4−2S6
View SolutionIf →a and →b are unit vectors inclined at an angle θ then the value of ∣∣→a−→b∣∣ is a.2sin(θ2) b. 2sinθ c. 2cos(θ2) d. 2 cosθ
View SolutionWhen two vectors of magnitudes P and Q are inclined at an angle θ, the magnitudes of their resultant is 2P. When the inclination is changed to 180∘−θ, the magnitudes of the resultant is halved. Find the ratio of P and Q.
View SolutionIf ∣∣→A∣∣=2and∣∣→B∣∣=4, then match the relations in column I with the angleθ between →Aand→B in column II.
Column I, Column II
(a) ∣∣→A×→B∣∣=0 , (i) θ=30∘
(b) ∣∣→A×→B∣∣=0 , (ii) θ=45∘
(c ) →A×→B∣=4 , (iii) θ=90∘
(d) ∣∣→A×x→B∣∣=4√2 , (iv) θ=0∘.
View SolutionIf →a=(3,1)and→b=(1,2) represent the sides of a parallelogram then the angle θ between the diagonals of the paralelogram is given by (A) θ=cos−1(1√5) (B) θ=cos−1(2√5) (C) θ=cos−1(12√5) (D) θ=π2
View SolutionIf tanθ+sinθ=m and tanθ−sinθ=n then prove m2−n2=4√mn
View Solution
