What is correct ?
|a−b|=|a|−|b|
|a−b|≤|a|−|b|
|a−b|≥|a|−|b|
|a−b|>|a|−|b|
The correct Answer is:C
To solve the question regarding the properties of the modulus of vectors, we need to analyze the given options step by step.
1. Understanding the Modulus of Vectors:
The modulus (or magnitude) of a vector a is denoted as |a|. The question involves the expression |a−b|.
2. Applying the Triangle Inequality:
The triangle inequality states that for any vectors a and b:
|a+b|≤|a|+|b|
and
|a−b|≥||a|−|b||
This means that:
|a−b|≥||a|−|b||
3. Analyzing the Options:
- Option A: |a−b|=|a|−|b| - This is not generally true.
- Option B: |a−b|≤|a|−|b| - This contradicts the triangle inequality and is false.
- Option C: |a−b|≥|a|−|b| - This is true based on the triangle inequality.
- Option D: |a−b|>|a|−|b| - This may be true in some cases but is not universally applicable.
4. Conclusion:
Based on the analysis, the correct answer is Option C: |a−b|≥|a|−|b|.
Final Answer:
The correct option is C: |a−b|≥|a|−|b|.
The modulus (or magnitude) of a vector a is denoted as |a|. The question involves the expression |a−b|.
The triangle inequality states that for any vectors a and b:
|a+b|≤|a|+|b|
and
|a−b|≥||a|−|b||
This means that:
|a−b|≥||a|−|b||
- Option A: |a−b|=|a|−|b| - This is not generally true.
- Option B: |a−b|≤|a|−|b| - This contradicts the triangle inequality and is false.
- Option C: |a−b|≥|a|−|b| - This is true based on the triangle inequality.
- Option D: |a−b|>|a|−|b| - This may be true in some cases but is not universally applicable.
Based on the analysis, the correct answer is Option C: |a−b|≥|a|−|b|.
The correct option is C: |a−b|≥|a|−|b|.
Topper's Solved these Questions
Similar Questions
Knowledge Check
What are correct steps to convert acetaldehyde to acetone?
ACH3MgBr,H2O,OxidationBOxidation, Ca(OH)2, HeatCReduction, KCN, HydrolysisDOxidation C2H5ONa, heat
What is the correct order of electronegativity?
View SolutionWhat is the correct order of density ?
View SolutionWhat is the correct order of pKa?
View SolutionWhat is the correct IUPAC name of
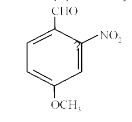 ?
?
View SolutionWhat is not correct about mitosis ?
View SolutionWhat is the correct order of electronegativity?
View SolutionWhat is the correct sequence of sperm formation?
View Solution